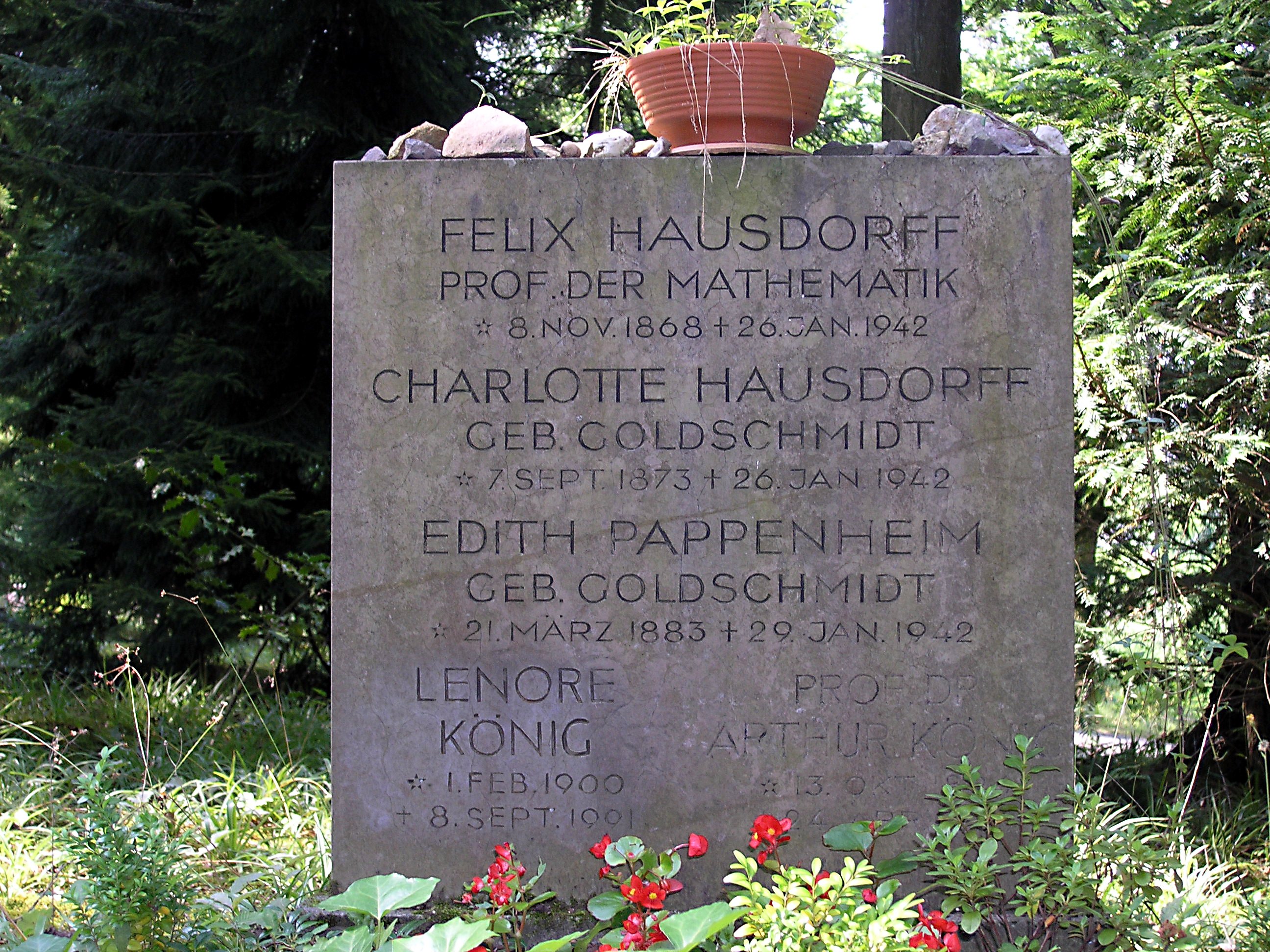|
Bernstein's Theorem On Monotone Functions
In real analysis, a branch of mathematics, Bernstein's theorem states that every real number, real-valued function (mathematics), function on the half-line that is totally monotone is a mixture of exponential functions. In one important special case the mixture is a weighted average, or expected value. Total monotonicity (sometimes also ''complete monotonicity'') of a function means that is continuous function, continuous on , infinitely differentiable on , and satisfies (-1)^n \frac f(t) \geq 0 for all nonnegative integers and for all . Another convention puts the opposite inequality (mathematics), inequality in the above definition. The "weighted average" statement can be characterized thus: there is a non-negative finite Borel measure on with cumulative distribution function such that f(t) = \int_0^\infty e^ \, dg(x), the integral being a Riemann–Stieltjes integral. In more abstract language, the theorem characterises Laplace transforms of positive Borel measures on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Analysis
In mathematics, the branch of real analysis studies the behavior of real numbers, sequences and series of real numbers, and real functions. Some particular properties of real-valued sequences and functions that real analysis studies include convergence, limits, continuity, smoothness, differentiability and integrability. Real analysis is distinguished from complex analysis, which deals with the study of complex numbers and their functions. Scope Construction of the real numbers The theorems of real analysis rely on the properties of the (established) real number system. The real number system consists of an uncountable set (\mathbb), together with two binary operations denoted and \cdot, and a total order denoted . The operations make the real numbers a field, and, along with the order, an ordered field. The real number system is the unique '' complete ordered field'', in the sense that any other complete ordered field is isomorphic to it. Intuitively, completenes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zoran Vondraček
Zoran Vondraček (born July 28, 1959) is a Croatian mathematician specializing in Lévy processes, transformed Brownian motions, and probabilistic potential theory. He is a professor of mathematics at the University of Zagreb. Education and career Vondraček graduated from the University of Zagreb in 1982, and obtained a master's degree in mathematics there in 1986. He completed a Ph.D. at the University of Florida in 1990 under the supervision of Murali Rao. In 1992 Vondraček was made assistant professor of mathematics at the University of Zagreb. He became an associate professor in 1997, and a full professor in 2002. Vondraček is a member of the Croatian Academy of Sciences and Arts, the American Mathematical Society The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, ..., and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolutely And Completely Monotonic Functions And Sequences
In mathematics, the notions of an absolutely monotonic function and a completely monotonic function are two very closely related concepts. Both imply very strong monotonicity properties. Both types of functions have derivatives of all orders. In the case of an absolutely monotonic function, the function as well as its derivatives of all orders must be non-negative in its domain of definition which would imply that the function as well as its derivatives of all orders are monotonically increasing functions in the domain of definition. In the case of a completely monotonic function, the function and its derivatives must be alternately non-negative and non-positive in its domain of definition which would imply that function and its derivatives are alternately monotonically increasing and monotonically decreasing functions. Such functions were first studied by S. Bernshtein in 1914 and the terminology is also due to him. There are several other related notions like the concepts of alm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Moment Problem
In mathematics, the Hausdorff moment problem, named after Felix Hausdorff, asks for necessary and sufficient conditions that a given sequence be the sequence of moments :m_n = \int_0^1 x^n\,d\mu(x) of some Borel measure supported on the closed unit interval . In the case , this is equivalent to the existence of a random variable supported on , such that . The essential difference between this and other well-known moment problems is that this is on a bounded interval, whereas in the Stieltjes moment problem one considers a half-line , and in the Hamburger moment problem one considers the whole line . The Stieltjes moment problems and the Hamburger moment problems, if they are solvable, may have infinitely many solutions (indeterminate moment problem) whereas a Hausdorff moment problem always has a unique solution if it is solvable (determinate moment problem). In the indeterminate moment problem case, there are infinite measures corresponding to the same prescribed moment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Monotonicity
In mathematics, the Hausdorff moment problem, named after Felix Hausdorff, asks for necessary and sufficient conditions that a given sequence be the sequence of moments :m_n = \int_0^1 x^n\,d\mu(x) of some Borel measure supported on the closed unit interval . In the case , this is equivalent to the existence of a random variable supported on , such that . The essential difference between this and other well-known moment problems is that this is on a bounded interval, whereas in the Stieltjes moment problem one considers a half-line , and in the Hamburger moment problem one considers the whole line . The Stieltjes moment problems and the Hamburger moment problems, if they are solvable, may have infinitely many solutions (indeterminate moment problem) whereas a Hausdorff moment problem always has a unique solution if it is solvable (determinate moment problem). In the indeterminate moment problem case, there are infinite measures corresponding to the same prescribed moments an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Hausdorff
Felix Hausdorff ( , ; November 8, 1868 – January 26, 1942) was a German mathematician, pseudonym Paul Mongré (''à mogré' (Fr.) = "according to my taste"), who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, and functional analysis. Hausdorff was Jewish, and life became difficult for him and his family after the '' Kristallnacht'' of 1938. The next year he initiated efforts to emigrate to the United States, but was unable to make arrangements to receive a research fellowship. On 26 January 1942, Hausdorff, along with his wife and his sister-in-law, died by suicide by taking an overdose of veronal, rather than comply with German orders to move to the Endenich camp, and there suffer the likely implications, about which he held no illusions. Life Childhood and youth Hausdorff's father, the Jewish merchant Louis Hausdorff (1843–1896), moved with his young family to Leipzig in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex-valued frequency domain, also known as ''s''-domain, or ''s''-plane). The transform is useful for converting derivative, differentiation and integral, integration in the time domain into much easier multiplication and Division (mathematics), division in the Laplace domain (analogous to how logarithms are useful for simplifying multiplication and division into addition and subtraction). This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic equation, algebraic polynomial equations, and by simplifyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann–Stieltjes Integral
In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes. The definition of this integral was first published in 1894 by Stieltjes. It serves as an instructive and useful precursor of the Lebesgue integral, and an invaluable tool in unifying equivalent forms of statistical theorems that apply to discrete and continuous probability. Formal definition The Riemann–Stieltjes integral of a real-valued function f of a real variable on the interval ,b/math> with respect to another real-to-real function g is denoted by :\int_^b f(x) \, \mathrmg(x). Its definition uses a sequence of partitions P of the interval ,b/math> :P=\. The integral, then, is defined to be the limit, as the mesh (the length of the longest subinterval) of the partitions approaches 0 , of the approximating sum :S(P,f,g) = \sum_^ f(c_i)\left g(x_) - g(x_) \right/math> where c_i is in the i-th subinterval _,x_/math> ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |