|
Barnard's Test
In statistics, Barnard’s test is an exact test used in the analysis of contingency tables with one margin fixed. Barnard’s tests are really a class of hypothesis tests, also known as unconditional exact tests for two independent binomials. These tests examine the association of two categorical variables and are often a more powerful alternative than Fisher's exact test for contingency tables. While first published in 1945 by G.A. Barnard, the test did not gain popularity due to the computational difficulty of calculating the value and Fisher’s specious disapproval. Nowadays, for small / moderate sample sizes computers can often implement Barnard’s test in a few seconds. Purpose and scope Barnard’s test is used to test the independence of rows and columns in a contingency table. The test assumes each response is independent. Under independence, there are three types of study designs that yield a table, and Barnard's test applies to the second type. To distin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided dice rolled ''n'' times. For ''n'' independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the prefix, and ''k'' the suffix). The Bernoulli distribution models the outcome of a single Bernoulli tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boschloo's Test
Boschloo's test is a statistical hypothesis test for analysing 2x2 contingency tables. It examines the association of two Bernoulli distributed random variables and is a uniformly more powerful alternative to Fisher's exact test. It was proposed in 1970 by R. D. Boschloo. Setting A 2x2 contingency table visualizes n independent observations of two binary variables A and B: : \begin & B = 1 & B = 0 & \mbox\\ \hline A = 1 & x_ & x_ & n_1 \\ A = 0 & x_ & x_ & n_0 \\ \hline \mbox & s_1 & s_0 & n\\ \end The probability distribution of such tables can be classified into three distinct cases. # The row sums n_1, n_0 and column sums s_1, s_0 are fixed in advance and not random. Then all x_ are determined by x_. If A and B are independent, x_ follows a hypergeometric distribution with parameters n, n_1, s_1: x_ \sim \mbox(n, n_1, s_1). # The row sums n_1, n_0 are fixed in advance but the column sums s_1, s_0 are not. Then all random parameters are determined by x_ and x_ and x_, x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type I And Type II Errors
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unlu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancillary Statistic
An ancillary statistic is a measure of a sample whose distribution (or whose pmf or pdf) does not depend on the parameters of the model. An ancillary statistic is a pivotal quantity that is also a statistic. Ancillary statistics can be used to construct prediction intervals. This concept was introduced by Ronald Fisher in the 1920s. Examples Suppose ''X''1, ..., ''X''''n'' are independent and identically distributed, and are normally distributed with unknown expected value ''μ'' and known variance 1. Let :\overline_n = \frac be the sample mean. The following statistical measures of dispersion of the sample *Range: max(''X''1, ..., ''X''''n'') − min(''X''1, ..., ''Xn'') *Interquartile range: ''Q''3 − ''Q''1 *Sample variance: :: \hat^2:=\,\frac are all ''ancillary statistics'', because their sampling distributions do not change as ''μ'' changes. Computationally, this is because in the formulas, the ''μ'' terms cancel – adding a constant number to a distributio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuisance Parameter
Nuisance (from archaic ''nocence'', through Fr. ''noisance'', ''nuisance'', from Lat. ''nocere'', "to hurt") is a common law tort. It means that which causes offence, annoyance, trouble or injury. A nuisance can be either public (also "common") or private. A public nuisance was defined by English scholar Sir James Fitzjames Stephen as, "an act not warranted by law, or an omission to discharge a legal duty, which act or omission obstructs or causes inconvenience or damage to the public in the exercise of rights common to all Her Majesty's subjects". ''Private nuisance'' is the interference with the right of specific people. Nuisance is one of the oldest causes of action known to the common law, with cases framed in nuisance going back almost to the beginning of recorded case law. Nuisance signifies that the "right of quiet enjoyment" is being disrupted to such a degree that a tort is being committed. Definition Under the common law, persons in possession of real property (lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
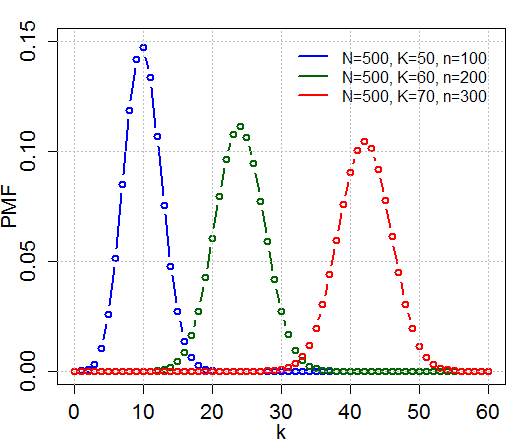
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ('' sampling without replacement'' from a finite population). A random variable X follows the hype ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Distribution
In probability theory and statistics, the binomial distribution with parameters ''n'' and ''p'' is the discrete probability distribution of the number of successes in a sequence of ''n'' independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: ''success'' (with probability ''p'') or ''failure'' (with probability q=1-p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., ''n'' = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance. The binomial distribution is frequently used to model the number of successes in a sample of size ''n'' drawn with replacement from a population of size ''N''. If the sampling is carried out without replacement, the draws are not independent and so the resultin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory. If X_1, X_2, \dots, X_n, \dots are random samples drawn from a population with overall mean \mu and finite variance and if \bar_n is the sample mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson's Chi-squared Test
Pearson's chi-squared test (\chi^2) is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to ''Pearson χ-squared'' test or statistic are used. It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the modern synthesis. For his contributions to biology, Fisher has been called "the greatest of Darwin’s successors". Fisher held strong views on race and eugenics, insisting on racial differences. Although he was clearly a eugenist and advocated for the legalization of voluntary sterilization of those with heritable mental disabilities, there is some debate as to whether Fisher support ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |