|
Banach's Matchbox Problem
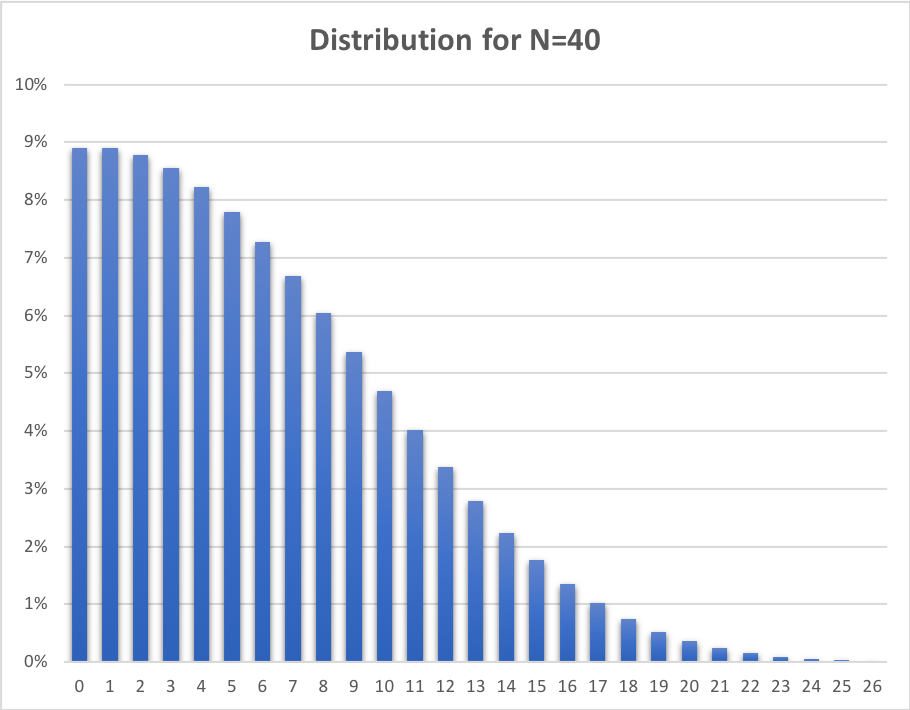
Banach's match problem is a classic problem in probability attributed to Stefan Banach. Feller says that the problem was inspired by a humorous reference to Banach's smoking habit in a speech honouring him by Hugo Steinhaus, but that it was not Banach who set the problem or provided an answer. Suppose a mathematician carries two matchboxes at all times: one in his left pocket and one in his right. Each time he needs a match, he is equally likely to take it from either pocket. Suppose he reaches into his pocket and discovers for the first time that the box picked is empty. If it is assumed that each of the matchboxes originally contained N matches, what is the probability that there are exactly k matches in the other box? Solution Without loss of generality consider the case where the matchbox in his right pocket has an unlimited number of matches and let M be the number of matches removed from this one before the left one is found to be empty. When the left pocket is found to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan Banach
Stefan Banach ( ; 30 March 1892 – 31 August 1945) was a Polish mathematician who is generally considered one of the 20th century's most important and influential mathematicians. He was the founder of modern functional analysis, and an original member of the Lwów School of Mathematics. His major work was the 1932 book, ''Théorie des opérations linéaires'' (Theory of Linear Operations), the first monograph on the general theory of functional analysis. Born in Kraków to a family of Goral descent, Banach showed a keen interest in mathematics and engaged in solving mathematical problems during school recess. After completing his secondary education, he befriended Hugo Steinhaus, with whom he established the Polish Mathematical Society in 1919 and later published the scientific journal '' Studia Mathematica''. In 1920, he received an assistantship at the Lwów Polytechnic, subsequently becoming a professor in 1922 and a member of the Polish Academy of Learning in 1924. Banach ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hugo Steinhaus
Hugo Dyonizy Steinhaus ( ; ; January 14, 1887 – February 25, 1972) was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the Jan Kazimierz University in Lwów (now Lviv, Ukraine), where he helped establish what later became known as the Lwów School of Mathematics. He is credited with "discovering" mathematician Stefan Banach, with whom he gave a notable contribution to functional analysis through the Banach–Steinhaus theorem. After World War II Steinhaus played an important part in the establishment of the mathematics department at Wrocław University and in the revival of Polish mathematics from the destruction of the war. Author of around 170 scientific articles and books, Steinhaus has left his legacy and contribution in many branches of mathematics, such as functional analysis, geometry, mathematical logic, and trigonometry. Notably he is regarded as one of the early found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Binomial Distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of successes (denoted r) occurs. For example, we can define rolling a 6 on a die as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success (r=3). In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution. An alternative formulation is to model the number of total trials (instead of the number of failures). In fact, for a specified (non-random) number of successes (r), the number of failures (n - r) are random because the total trials (n) are random. For example, we could use the negative binomial distribution to model the number of days n (random) a certain machine works (specified by r) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Matchbox
Banach (pronounced in German, in Slavic Languages, and or in English) is a Jewish surname of Ashkenazi origin believed to stem from the translation of the phrase " son of man", combining the Hebrew word ''ben'' ("son of") and Arameic ''nasha'' ("man"). Worth mentioning is how the Sephardic surname ''Banache'' presents a variant with the ''-ache'' alternative ultima, common in other Jewish surnames such as ''Farache'', '' Ayache'', ''Nakache'', ''Harache'' or ''Marrache''. Notable people with this surname include: * Stefan Banach (1892–1945), Polish mathematician * Ed Banach (born 1960), American wrestler * Lou Banach (born 1960), American wrestler *Korneliusz Banach (born 25 January 1994), Polish volleyball player * Łukasz Banach, birth name of Norman Leto (born 1980), Polish artist in the fields of painting, film, and new media *Maurice Banach, German footballer *Orest Banach Orest “Orri” Banach ( ua, Орест (Оррі) Банах) is a retired German-American ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stirling's Approximation
In mathematics, Stirling's approximation (or Stirling's formula) is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre. One way of stating the approximation involves the logarithm of the factorial: \ln(n!) = n\ln n - n +O(\ln n), where the big O notation means that, for all sufficiently large values of n, the difference between \ln(n!) and n\ln n-n will be at most proportional to the logarithm. In computer science applications such as the worst-case lower bound for comparison sorting, it is convenient to use instead the binary logarithm, giving the equivalent form \log_2 (n!) = n\log_2 n - n\log_2 e +O(\log_2 n). The error term in either base can be expressed more precisely as \tfrac12\log(2\pi n)+O(\tfrac1n), corresponding to an approximate formula for the factorial itself, n! \sim \sqrt\left(\frac\righ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Things Named After Stefan Banach
Stefan Banach was a Polish mathematician who made key contributions to mathematics. This article contains some of the things named in his memory. Mathematics * Banach algebra ** Amenable Banach algebra * Banach Jordan algebra ** Banach function algebra **Banach *-algebra ** Banach algebra cohomology * Banach bundle ** Banach bundle (non-commutative geometry) * Banach fixed-point theorem *Banach game *Banach lattice * Banach limit * Banach manifold * Banach measure * Banach space ** Banach coordinate space ** Banach disks **Banach norm * Banach–Alaoglu theorem * Banach–Mazur compactum * Banach–Mazur game * Banach–Mazur theorem * Banach–Ruziewicz problem * Banach-Saks theorem * Banach-Schauder theorem * Banach–Steinhaus theorem * Banach–Stone theorem * Banach–Tarski paradox * Banach's matchbox problem * Hahn–Banach theorem Other * 16856 Banach * Banach Journal of Mathematical Analysis * International Stefan Banach Prize *Stefan Banach Medal Stefan B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Probability
Applied probability is the application of probability theory to statistical problems and other scientific and engineering domains. Scope Much research involving probability is done under the auspices of applied probability. However, while such research is motivated (to some degree) by applied problems, it is usually the mathematical aspects of the problems that are of most interest to researchers (as is typical of applied mathematics in general). Applied probabilists are particularly concerned with the application of stochastic processes, and probability more generally, to the natural, applied and social sciences, including biology, physics (including astronomy), chemistry, medicine, computer science and information technology, and economics. Another area of interest is in engineering: particularly in areas of uncertainty, risk management, probabilistic design, and Quality assurance. See also *Areas of application: **Ruin theory **Statistical physics **Stoichiometry and modelli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Probability")
