|
Balinski's Theorem
In polyhedral combinatorics, a branch of mathematics, Balinski's theorem is a statement about the graph-theoretic structure of three-dimensional convex polyhedra and higher-dimensional convex polytopes. It states that, if one forms an undirected graph from the vertices and edges of a convex ''d''-dimensional convex polyhedron or polytope (its skeleton), then the resulting graph is at least ''d''-vertex-connected: the removal of any ''d'' − 1 vertices leaves a connected subgraph. For instance, for a three-dimensional polyhedron, even if two of its vertices (together with their incident edges) are removed, for any pair of vertices there will still exist a path of vertices and edges connecting the pair. Balinski's theorem is named after mathematician Michel Balinski, who published its proof in 1961, although the three-dimensional case dates back to the earlier part of the 20th century and the discovery of Steinitz's theorem that the graphs of three-dimensional polyhed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pacific Journal Of Mathematics
The Pacific Journal of Mathematics is a mathematics research journal supported by several universities and research institutes, and currently published on their behalf by Mathematical Sciences Publishers, a non-profit academic publishing organisation, and the University of California, Berkeley. It was founded in 1951 by František Wolf and Edwin F. Beckenbach and has been published continuously since, with five two-issue volumes per year and 12 issues per year. Full-text PDF versions of all journal articles are available on-line via the journal's website with a subscription. The journal is incorporated as a 501(c)(3) organization. References Mathematics journals Publications established in 1951 Mathematical Sciences Publishers academic journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
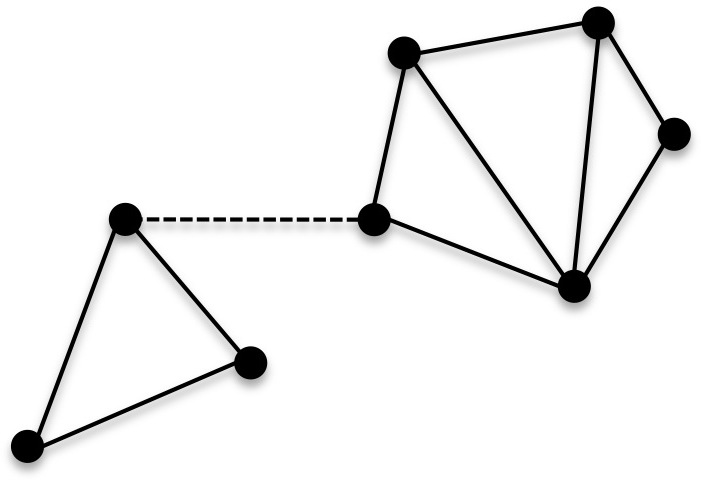
Graph Connectivity
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent. A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertices i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes. Research in polyhedral combinatorics falls into two distinct areas. Mathematicians in this area study the combinatorics of polytopes; for instance, they seek inequalities that describe the relations between the numbers of vertices, edges, and faces of higher dimensions in arbitrary polytopes or in certain important subclasses of polytopes, and study other combinatorial properties of polytopes such as their connectivity and diameter (number of steps needed to reach any vertex from any other vertex). Additionally, many computer scientists use the phrase “polyhedral combinatorics” to describe research into precise descriptions of the faces of certain specific polytopes (especially 0-1 polytopes, whose vertices are subsets of a hypercube) arising from integer progr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex Method
In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming. The name of the algorithm is derived from the concept of a simplex and was suggested by T. S. Motzkin. Simplices are not actually used in the method, but one interpretation of it is that it operates on simplicial ''cones'', and these become proper simplices with an additional constraint. The simplicial cones in question are the corners (i.e., the neighborhoods of the vertices) of a geometric object called a polytope. The shape of this polytope is defined by the constraints applied to the objective function. History George Dantzig worked on planning methods for the US Army Air Force during World War II using a desk calculator. During 1946 his colleague challenged him to mechanize the planning process to distract him from taking another job. Dantzig formulated the problem as linear inequalities inspired by the work of Wassily Leontief, however, at that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klein's Encyclopedia
Felix Klein's ''Encyclopedia of Mathematical Sciences'' is a German mathematical Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ... encyclopedia published in six volumes from 1898 to 1933. Klein and Wilhelm Franz Meyer were organizers of the encyclopedia. Its full title in English is ''Encyclopedia of Mathematical Sciences Including Their Applications'', which is ''Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen'' (EMW). It is 20,000 pages in length (6 volumes, ''i.e. Bände'', published in 23 separate books, 1-1, 1-2, 2-1-1, 2-1-2, 2-2, 2-3-1, 2-3-2, 3-1-1, 3-1-2, 3-2-1, 3-2-2a, 3-2-2b, 3-3, 4-1, 4-2, 4-3, 4-4, 5-1, 5-2, 5-3, 6-1, 6-2-1, 6-2-2) and was published by B.G. Teubner Verlag, publisher of ''Mathematische Annalen''. Today, Göttinger Digit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steinitz's Theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. This result provides a classification theorem for the three-dimensional convex polyhedra, something that is not known in higher dimensions. It provides a complete and purely combinatorial description of the graphs of these polyhedra, allowing other results on them, such as Eberhard's theorem on the realization of polyhedra with given types of faces, to be proven more easily, without reference to the geometry of these shapes. Additionally, it has been applied in graph drawing, as a way to construct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michel Balinski
Michel Louis Balinski (born Michał Ludwik Baliński; October 6, 1933 – February 4, 2019) was an applied mathematician, economist, operations research analyst and political scientist. As a Polish-American, educated in the United States, he lived and worked primarily in the United States and France. He was known for his work in optimisation (combinatorial, linear, nonlinear), convex polyhedra, stable matching, and the theory and practice of electoral systems, jury decision, and social choice. He was Directeur de Recherche de classe exceptionnelle (emeritus) of the C.N.R.S. at the École Polytechnique (Paris). He was awarded the John von Neumann Theory Prize by INFORMS in 2013. Michel Louis Balinski died in Bayonne, France. He maintained an active involvement in research and public appearances, his last public engagement took place in January 2019. Early life Michel Balinski was born in Geneva, Switzerland, the grandson of the Polish bacteriologist and founder of UNICEF, Lu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes. Research in polyhedral combinatorics falls into two distinct areas. Mathematicians in this area study the combinatorics of polytopes; for instance, they seek inequalities that describe the relations between the numbers of vertices, edges, and faces of higher dimensions in arbitrary polytopes or in certain important subclasses of polytopes, and study other combinatorial properties of polytopes such as their connectivity and diameter (number of steps needed to reach any vertex from any other vertex). Additionally, many computer scientists use the phrase “polyhedral combinatorics” to describe research into precise descriptions of the faces of certain specific polytopes (especially 0-1 polytopes, whose vertices are subsets of a hypercube) arising from integer progr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graduate Texts In Mathematics
Graduate Texts in Mathematics (GTM) (ISSN 0072-5285) is a series of graduate-level textbooks in mathematics published by Springer-Verlag. The books in this series, like the other Springer-Verlag mathematics series, are yellow books of a standard size (with variable numbers of pages). The GTM series is easily identified by a white band at the top of the book. The books in this series tend to be written at a more advanced level than the similar Undergraduate Texts in Mathematics series, although there is a fair amount of overlap between the two series in terms of material covered and difficulty level. List of books #''Introduction to Axiomatic Set Theory'', Gaisi Takeuti, Wilson M. Zaring (1982, 2nd ed., ) #''Measure and Category – A Survey of the Analogies between Topological and Measure Spaces'', John C. Oxtoby (1980, 2nd ed., ) #''Topological Vector Spaces'', H. H. Schaefer, M. P. Wolff (1999, 2nd ed., ) #''A Course in Homological Algebra'', Peter Hilton, Urs Stammbac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connectivity (graph Theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent. A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
