|
Autoregressive Fractionally Integrated Moving Average
In statistics, autoregressive fractionally integrated moving average models are time series models that generalize ARIMA (''autoregressive integrated moving average'') models by allowing non-integer values of the differencing parameter. These models are useful in modeling time series with long memory—that is, in which deviations from the long-run mean decay more slowly than an exponential decay. The acronyms "ARFIMA" or "FARIMA" are often used, although it is also conventional to simply extend the "ARIMA(''p'', ''d'', ''q'')" notation for models, by simply allowing the order of differencing, ''d'', to take fractional values. Basics In an ARIMA model, the ''integrated'' part of the model includes the differencing operator (1 − ''B'') (where ''B'' is the backshift operator) raised to an integer power. For example, :(1-B)^2=1-2B+B^2 \,, where :B^2X_t=X_ \, , so that :(1-B)^2X_t = X_t -2X_ + X_. In a ''fractional'' model, the power is allowed to be fractional, with the meaning of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forecasting' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ARIMA
Arima, officially The Royal Chartered Borough of Arima is the easternmost and second largest in area of the three boroughs of Trinidad and Tobago. It is geographically adjacent to Sangre Grande and Arouca at the south central foothills of the Northern Range. To the south is the Caroni–Arena Dam. Coterminous with Town of Arima since 1888, the borough of Arima is the fourth-largest municipality in population in the country (after Port of Spain, Chaguanas and San Fernando). The census estimated it had 33,606 residents in 2011. In 1887, the town petitioned Queen Victoria for municipal status as part of her Golden Jubilee celebration. This was granted in the following year, and Arima became a Royal Borough on 1 August 1888. Historically the third-largest town of Trinidad and Tobago, Arima is fourth since Chaguanas became the largest town in the country. Geography Climate The borough has a tropical rainforest climate (Köppen ''Af''), bordering on a tropical monsoon climate, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and the viscosities ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long-range Dependency
Long-range dependence (LRD), also called long memory or long-range persistence, is a phenomenon that may arise in the analysis of spatial or time series data. It relates to the rate of decay of statistical dependence of two points with increasing time interval or spatial distance between the points. A phenomenon is usually considered to have long-range dependence if the dependence decays more slowly than an exponential decay, typically a power-like decay. LRD is often related to self-similar processes or fields. LRD has been used in various fields such as internet traffic modelling, econometrics, hydrology, linguistics and the earth sciences. Different mathematical definitions of LRD are used for different contexts and purposes. Short-range dependence versus long-range dependence One way of characterising long-range and short-range dependent stationary process is in terms of their autocovariance functions. For a short-range dependent process, the coupling between values at differen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backshift Operator
In time series analysis, the lag operator (L) or backshift operator (B) operates on an element of a time series to produce the previous element. For example, given some time series :X= \ then : L X_t = X_ for all t > 1 or similarly in terms of the backshift operator ''B'': B X_t = X_ for all t > 1. Equivalently, this definition can be represented as : X_t = L X_ for all t \geq 1 The lag operator (as well as backshift operator) can be raised to arbitrary integer powers so that : L^ X_ = X_ and : L^k X_ = X_. Lag polynomials Polynomials of the lag operator can be used, and this is a common notation for ARMA (autoregressive moving average) models. For example, : \varepsilon_t = X_t - \sum_^p \varphi_i X_ = \left(1 - \sum_^p \varphi_i L^i\right) X_t specifies an AR(''p'') model. A polynomial of lag operators is called a lag polynomial so that, for example, the ARMA model can be concisely specified as : \varphi (L) X_t = \theta (L) \varepsilon_t where \varphi (L) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Series
In mathematics, the binomial series is a generalization of the polynomial that comes from a binomial formula expression like (1+x)^n for a nonnegative integer n. Specifically, the binomial series is the Taylor series for the function f(x)=(1+x)^ centered at x = 0, where \alpha \in \Complex and , x, 0 and diverges to +\infty if \operatorname\alpha<0. If , then converges if and only if the sequence converges , which is certainly true if but false if : in the latter case the sequence is dense , due to the fact that diverges and converges to zero). Summation of the binomial series The usual argument to compute the sum of the binomial series goes as follows.[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Brownian Motion
In probability theory, fractional Brownian motion (fBm), also called a fractal Brownian motion, is a generalization of Brownian motion. Unlike classical Brownian motion, the increments of fBm need not be independent. fBm is a continuous-time Gaussian process ''BH''(''t'') on , ''T'' that starts at zero, has expectation zero for all ''t'' in , ''T'' and has the following covariance function: :E _H(t) B_H (s)\tfrac (, t, ^+, s, ^-, t-s, ^), where ''H'' is a real number in (0, 1), called the Hurst index or Hurst parameter associated with the fractional Brownian motion. The Hurst exponent describes the raggedness of the resultant motion, with a higher value leading to a smoother motion. It was introduced by . The value of ''H'' determines what kind of process the ''fBm'' is: * if ''H'' = 1/2 then the process is in fact a Brownian motion or Wiener process; * if ''H'' > 1/2 then the increments of the process are positively correlated; * if ''H'' < 1/2 then the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autoregressive–moving-average Model
In the statistical analysis of time series, autoregressive–moving-average (ARMA) models provide a parsimonious description of a (weakly) stationary stochastic process in terms of two polynomials, one for the autoregression (AR) and the second for the moving average (MA). The general ARMA model was described in the 1951 thesis of Peter Whittle, ''Hypothesis testing in time series analysis'', and it was popularized in the 1970 book by George E. P. Box and Gwilym Jenkins. Given a time series of data X_t, the ARMA model is a tool for understanding and, perhaps, predicting future values in this series. The AR part involves regressing the variable on its own lagged (i.e., past) values. The MA part involves modeling the error term as a linear combination of error terms occurring contemporaneously and at various times in the past. The model is usually referred to as the ARMA(''p'',''q'') model where ''p'' is the order of the AR part and ''q'' is the order of the MA part (as defined b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
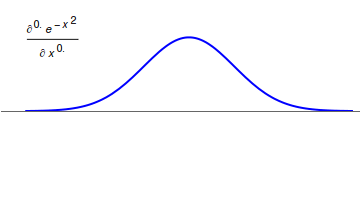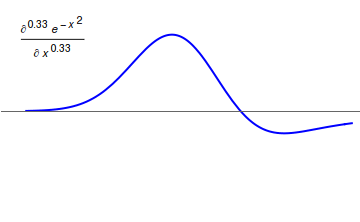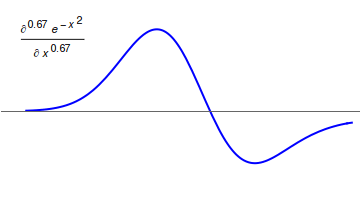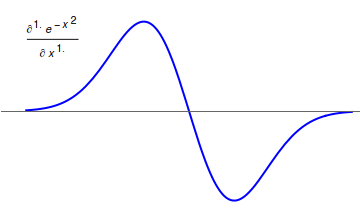
Differintegral
In fractional calculus, an area of mathematical analysis, the differintegral (sometime also called the derivigral) is a combined differentiation/integration operator. Applied to a function ƒ, the ''q''-differintegral of ''f'', here denoted by :\mathbb^q f is the fractional derivative (if ''q'' > 0) or fractional integral (if ''q'' So, \frac = \mathcal^\left\ which generalizes to \mathbb^qf(t) = \mathcal^\left\. Under the bilateral Laplace transform, here denoted by \mathcal and defined as \mathcal (t)=\int_^\infty e^ f(t)\, dt, differentiation transforms into a multiplication \mathcal\left frac\right= s\mathcal (t) Generalizing to arbitrary order and solving for \mathbb^qf(t), one obtains \mathbb^qf(t)=\mathcal^\left\. Representation via Newton series is the Newton interpolation over consecutive integer orders: \mathbb^qf(t) =\sum_^ \binom m \sum_^m\binom mk(-1)^f^(x). For fractional derivative definitions described in this section, the following identities hold: :\ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |