|
Arkadi Nemirovsky
Arkadi Nemirovski (born March 14, 1947) is a professor at the H. Milton Stewart School of Industrial and Systems Engineering at the Georgia Institute of Technology. He has been a leader in continuous optimization and is best known for his work on the ellipsoid method, modern interior-point methods and robust optimization. Biography Nemirovski earned a Ph.D. in Mathematics in 1974 from Moscow State University and a Doctor of Sciences in Mathematics degree in 1990 from the Institute of Cybernetics of the Ukrainian Academy of Sciences in Kiev. He has won three prestigious prizes: the Fulkerson Prize, the George B. Dantzig Prize, and the John von Neumann Theory Prize. He was elected a member of the U.S. National Academy of Engineering (NAE) in 2017 "for the development of efficient algorithms for large-scale convex optimization problems", and the U.S National Academy of Sciences (NAS) in 2020. Academic work Nemirovski first proposed mirror descent along with David Yudin in 1983. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moscow State University
M. V. Lomonosov Moscow State University (MSU; russian: Московский государственный университет имени М. В. Ломоносова) is a public research university in Moscow, Russia and the most prestigious university in the country. The university includes 15 research institutes, 43 faculties, more than 300 departments, and six branches (including five foreign ones in the Commonwealth of Independent States countries). Alumni of the university include past leaders of the Soviet Union and other governments. As of 2019, 13 List of Nobel laureates, Nobel laureates, six Fields Medal winners, and one Turing Award winner had been affiliated with the university. The university was ranked 18th by ''The Three University Missions Ranking'' in 2022, and 76th by the ''QS World University Rankings'' in 2022, #293 in the world by the global ''Times Higher World University Rankings'', and #326 by ''U.S. News & World Report'' in 2022. It was the highest-ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
National Academy Of Engineering
The National Academy of Engineering (NAE) is an American nonprofit, non-governmental organization. The National Academy of Engineering is part of the National Academies of Sciences, Engineering, and Medicine, along with the National Academy of Sciences (NAS), the National Academy of Medicine, and the National Research Council (now the program units of NASEM). The NAE operates engineering programs aimed at meeting national needs, encourages education and research, and recognizes the superior achievements of engineers. New members are annually elected by current members, based on their distinguished and continuing achievements in original research. The NAE is autonomous in its administration and in the selection of its members, sharing with the rest of the National Academies the role of advising the federal government. History The National Academy of Sciences was created by an Act of Incorporation dated March 3, 1863, which was signed by then President of the United States ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Living People
Related categories * :Year of birth missing (living people) / :Year of birth unknown * :Date of birth missing (living people) / :Date of birth unknown * :Place of birth missing (living people) / :Place of birth unknown * :Year of death missing / :Year of death unknown * :Date of death missing / :Date of death unknown * :Place of death missing / :Place of death unknown * :Missing middle or first names See also * :Dead people * :Template:L, which generates this category or death years, and birth year and sort keys. : {{DEFAULTSORT:Living people 21st-century people People by status ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Footnotes
A note is a string of text placed at the bottom of a page in a book or document or at the end of a chapter, volume, or the whole text. The note can provide an author's comments on the main text or citations of a reference work in support of the text. Footnotes are notes at the foot of the page while endnotes are collected under a separate heading at the end of a chapter, volume, or entire work. Unlike footnotes, endnotes have the advantage of not affecting the layout of the main text, but may cause inconvenience to readers who have to move back and forth between the main text and the endnotes. In some editions of the Bible, notes are placed in a narrow column in the middle of each page between two columns of biblical text. Numbering and symbols In English, a footnote or endnote is normally flagged by a superscripted number immediately following that portion of the text the note references, each such footnote being numbered sequentially. Occasionally, a number between brack ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aharon Ben-Tal
Aharon אַהֲרֹן is masculine given name alternate spelling, commonly in Israel, of ''Aaron'', prominent biblical figure in the Old Testament, "Of the Mountains", or "Mountaineer". There are other variants including "Ahron" and "Aron". Aharon is also occasionally a patronymic surname, usually with the hyphenated prefix "Ben-". People with the name include: Given name * Aharon Abuhatzira (1938–2021), Israeli politician * Aharon Amar (born 1937), Israeli footballer * Aharon Amir (1923–2008), Israeli poet, translator, and writer * Aharon Amram (born 1939), Israeli singer, composer, poet, and researcher * Aharon Appelfeld (1932–2018), Israeli novelist and Holocaust survivor * Aharon April (1932–2020), Russian artist * Aharon Barak (born 1936), Israeli lawyer and jurist * Aharon Becker (1905–1995), Israeli politician * Aharon Ben-Shemesh (1889–1988), Israeli writer, translator, and lecturer * Aharon Chelouche (1840–1920), Algerian landowner, jeweler, and moneychange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a single-variable function defined for a real variable , the function's derivative , and an initial guess for a root of . If the function satisfies sufficient assumptions and the initial guess is close, then :x_ = x_0 - \frac is a better approximation of the root than . Geometrically, is the intersection of the -axis and the tangent of the graph of at : that is, the improved guess is the unique root of the linear approximation at the initial point. The process is repeated as :x_ = x_n - \frac until a sufficiently precise value is reached. This algorithm is first in the class of Householder's methods, succeeded by Halley's method. The method can also be extended to complex functions an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-concordant Function
In optimization, a self-concordant function is a function f:\mathbb \rightarrow \mathbb for which : , f(x), \leq 2 f''(x)^ or, equivalently, a function f:\mathbb \rightarrow \mathbb that, wherever f''(x) > 0, satisfies : \left, \frac \frac \ \leq 1 and which satisfies f(x) = 0 elsewhere. More generally, a multivariate function f(x) : \mathbb^n \rightarrow \mathbb is self-concordant if : \left. \frac \nabla^2 f(x + \alpha y) \_ \preceq 2 \sqrt \, \nabla^2 f(x) or, equivalently, if its restriction to any arbitrary line is self-concordant. History As mentioned in the "Bibliography Comments" of their 1994 book, self-concordant functions were introduced in 1988 by Yurii Nesterov and further developed with Arkadi Nemirovski. As explained in their basic observation was that the Newton method is affine invariant, in the sense that if for a function f(x) we have Newton steps x_ = x_k - ''(x_k)f'(x_k) then for a function \phi(y) = f(Ay) where A is a non-degenerate linear trans ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
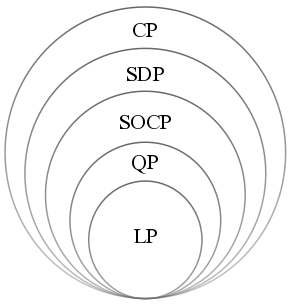
Semidefinite Programming
Semidefinite programming (SDP) is a subfield of convex optimization concerned with the optimization of a linear objective function (a user-specified function that the user wants to minimize or maximize) over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron. Semidefinite programming is a relatively new field of optimization which is of growing interest for several reasons. Many practical problems in operations research and combinatorial optimization can be modeled or approximated as semidefinite programming problems. In automatic control theory, SDPs are used in the context of linear matrix inequalities. SDPs are in fact a special case of cone programming and can be efficiently solved by interior point methods. All linear programs and (convex) quadratic programs can be expressed as SDPs, and via hierarchies of SDPs the solutions of polynomial optimization problems can be approximated. Semidefinite programming has been use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics ( optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible set is a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior Point Method
Interior-point methods (also referred to as barrier methods or IPMs) are a certain class of algorithms that solve linear and nonlinear convex optimization problems. An interior point method was discovered by Soviet mathematician I. I. Dikin in 1967 and reinvented in the U.S. in the mid-1980s. In 1984, Narendra Karmarkar developed a method for linear programming called Karmarkar's algorithm, which runs in provably polynomial time and is also very efficient in practice. It enabled solutions of linear programming problems that were beyond the capabilities of the simplex method. Contrary to the simplex method, it reaches a best solution by traversing the interior of the feasible region. The method can be generalized to convex programming based on a self-concordant barrier function used to encode the convex set. Any convex optimization problem can be transformed into minimizing (or maximizing) a linear function over a convex set by converting to the epigraph form. The idea of encodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |