|
Aristotelian Logic
In philosophy, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly by his followers, the Peripatetics. It was revived after the third century CE by Porphyry's Isagoge. Term logic revived in medieval times, first in Islamic logic by Alpharabius in the tenth century, and later in Christian Europe in the twelfth century with the advent of new logic, remaining dominant until the advent of predicate logic in the late nineteenth century. However, even if eclipsed by newer logical systems, term logic still plays a significant role in the study of logic. Rather than radically breaking with term logic, modern logics typically expand it, so to understand the newer systems, one must be acquainted with the earlier one. Aristotle's system Aristotle's logical work is collected in the six texts that are collectively known as the ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophy
Philosophy (from , ) is the systematized study of general and fundamental questions, such as those about existence, reason, knowledge, values, mind, and language. Such questions are often posed as problems to be studied or resolved. Some sources claim the term was coined by Pythagoras ( BCE), although this theory is disputed by some. Philosophical methods include questioning, critical discussion, rational argument, and systematic presentation. in . Historically, ''philosophy'' encompassed all bodies of knowledge and a practitioner was known as a ''philosopher''."The English word "philosophy" is first attested to , meaning "knowledge, body of knowledge." "natural philosophy," which began as a discipline in ancient India and Ancient Greece, encompasses astronomy, medicine, and physics. For example, Newton's 1687 ''Mathematical Principles of Natural Philosophy'' later became classified as a book of physics. In the 19th century, the growth of modern research universiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inference
Inferences are steps in reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in Europe dates at least to Aristotle (300s BCE). Deduction is inference deriving logical conclusions from premises known or assumed to be true, with the laws of valid inference being studied in logic. Induction is inference from particular evidence to a universal conclusion. A third type of inference is sometimes distinguished, notably by Charles Sanders Peirce, contradistinguishing abduction from induction. Various fields study how inference is done in practice. Human inference (i.e. how humans draw conclusions) is traditionally studied within the fields of logic, argumentation studies, and cognitive psychology; artificial intelligence researchers develop automated inference systems to emulate human inference. Statistical inference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truth
Truth is the property of being in accord with fact or reality.Merriam-Webster's Online Dictionarytruth 2005 In everyday language, truth is typically ascribed to things that aim to represent reality or otherwise correspond to it, such as beliefs, propositions, and declarative sentences. Truth is usually held to be the opposite of falsehood. The concept of truth is discussed and debated in various contexts, including philosophy, art, theology, and science. Most human activities depend upon the concept, where its nature as a concept is assumed rather than being a subject of discussion; these include most of the sciences, law, journalism, and everyday life. Some philosophers view the concept of truth as basic, and unable to be explained in any terms that are more easily understood than the concept of truth itself. Most commonly, truth is viewed as the correspondence of language or thought to a mind-independent world. This is called the correspondence theory of truth. Various theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
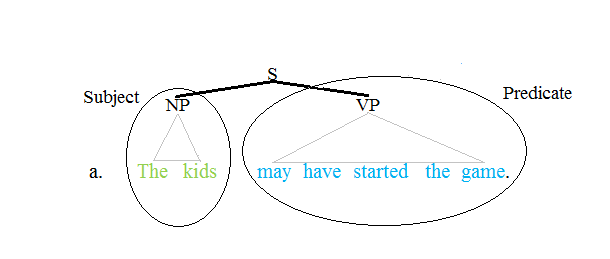
Subject (grammar)
The subject in a simple English sentence such as ''John runs'', ''John is a teacher'', or ''John drives a car'', is the person or thing about whom the statement is made, in this case ''John''. Traditionally the subject is the word or phrase which controls the verb in the clause, that is to say with which the verb agrees (''John is'' but ''John and Mary are''). If there is no verb, as in ''John what an idiot!'', or if the verb has a different subject, as in ''John I can't stand him!'', then 'John' is not considered to be the grammatical subject, but can be described as the ''topic'' of the sentence. While these definitions apply to simple English sentences, defining the subject is more difficult in more complex sentences and in languages other than English. For example, in the sentence ''It is difficult to learn French'', the subject seems to be the word ''it'', and yet arguably the real subject (the thing that is difficult) is ''to learn French''. A sentence such as ''It was J ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate (grammar)
The term predicate is used in one of two ways in linguistics and its subfields. The first defines a predicate as everything in a standard declarative sentence except the subject, and the other views it as just the main content verb or associated predicative expression of a clause. Thus, by the first definition the predicate of the sentence ''Frank likes cake'' is ''likes cake''. By the second definition, the predicate of the same sentence is just the content verb ''likes'', whereby ''Frank'' and ''cake'' are the arguments of this predicate. Differences between these two definitions can lead to confusion. Syntax Traditional grammar The notion of a predicate in traditional grammar traces back to Aristotelian logic. A predicate is seen as a property that a subject has or is characterized by. A predicate is therefore an expression that can be ''true of'' something. Thus, the expression "is moving" is true of anything that is moving. This classical understanding of predicates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categories (Aristotle)
The ''Categories'' (Greek Κατηγορίαι ''Katēgoriai''; Latin ''Categoriae'' or ''Praedicamenta'') is a text from Aristotle's ''Organon'' that enumerates all the possible kinds of things that can be the subject or the predicate of a proposition. They are "perhaps the single most heavily discussed of all Aristotelian notions". The work is brief enough to be divided, not into books as is usual with Aristotle's works, but into fifteen chapters. The ''Categories'' places every object of human apprehension under one of ten categories (known to medieval writers as the Latin term ''praedicamenta''). Aristotle intended them to enumerate everything that can be expressed without composition or structure, thus anything that can be either the subject or the predicate of a proposition. The text The antepraedicamenta The text begins with an explication of what Aristotle means by "synonymous", or univocal words, what is meant by "homonymous", or equivocal words, and what is mean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reasoning
Reason is the capacity of consciously applying logic by drawing conclusions from new or existing information, with the aim of seeking the truth. It is closely associated with such characteristically human activities as philosophy, science, language, mathematics, and art, and is normally considered to be a distinguishing ability possessed by humans. Reason is sometimes referred to as rationality. Reasoning is associated with the acts of thinking and cognition, and involves the use of one's intellect. The field of logic studies the ways in which humans can use formal reasoning to produce logically valid arguments. Reasoning may be subdivided into forms of logical reasoning, such as: deductive reasoning, inductive reasoning, and abductive reasoning. Aristotle drew a distinction between logical discursive reasoning (reason proper), and intuitive reasoning, in which the reasoning process through intuition—however valid—may tend toward the personal and the subjectively opaq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symbol (formal)
A logical symbol is a fundamental concept in logic, tokens of which may be marks or a configuration of marks which form a particular pattern. Although the term "symbol" in common use refers at some times to the idea being symbolized, and at other times to the marks on a piece of paper or chalkboard which are being used to express that idea; in the formal languages studied in mathematics and logic, the term "symbol" refers to the idea, and the marks are considered to be a token instance of the symbol. In logic, symbols build literal utility to illustrate ideas. Overview Symbols of a formal language need not be symbols ''of'' anything. For instance there are logical constants which do not refer to any idea, but rather serve as a form of punctuation in the language (e.g. parentheses). Symbols of a formal language must be capable of being specified without any reference to any interpretation of them. A symbol or string of symbols may comprise a well-formed formula if it is consis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propositions
In logic and linguistics, a proposition is the meaning of a declarative sentence. In philosophy, " meaning" is understood to be a non-linguistic entity which is shared by all sentences with the same meaning. Equivalently, a proposition is the non-linguistic bearer of truth or falsity which makes any sentence that expresses it either true or false. While the term "proposition" may sometimes be used in everyday language to refer to a linguistic statement which can be either true or false, the technical philosophical term, which differs from the mathematical usage, refers exclusively to the non-linguistic meaning behind the statement. The term is often used very broadly and can also refer to various related concepts, both in the history of philosophy and in contemporary analytic philosophy. It can generally be used to refer to some or all of the following: The primary bearers of truth values (such as "true" and "false"); the objects of belief and other propositional attitudes (i.e. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal System
A formal system is an abstract structure used for inferring theorems from axioms according to a set of rules. These rules, which are used for carrying out the inference of theorems from axioms, are the logical calculus of the formal system. A formal system is essentially an "axiomatic system". In 1921, David Hilbert proposed to use such a system as the foundation for the knowledge in mathematics. A formal system may represent a well-defined abstraction, system of abstract thought. The term ''formalism'' is sometimes a rough synonym for ''formal system'', but it also refers to a given style of notation, for example, Paul Dirac's bra–ket notation. Background Each formal system is described by primitive Symbol (formal), symbols (which collectively form an Alphabet (computer science), alphabet) to finitely construct a formal language from a set of axioms through inferential rules of formation. The system thus consists of valid formulas built up through finite combinations of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gisela Striker
Gisela Striker (born 1943) is a German classical scholar. She is Professor Emerita of Philosophy and Classics at Harvard University and a specialist in ancient Greek and Roman philosophy. Education and career Striker was born and educated in Germany, earning her doctorate in philosophy from the University of Göttingen under the supervision of Günther Patzig in 1969 and her Habilitation, also from Göttingen in 1978. She taught philosophy at Göttingen from 1971–1986, and then was professor of philosophy at Columbia University from 1986–1989, and then at Harvard from 1989–1997. In 1997, she became the sixth Laurence Professor of Ancient Philosophy at the University of Cambridge, England, serving until 2000, when she returned to Harvard. She expressed frustration with the ancient philosophy program at Harvard. Philosophical work Striker specializes in ancient philosophy, teaching Plato and Aristotle, as well as earlier and later Greek and Roman authors. She has written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timothy Smiley
Timothy John Smiley FBA (born 13 November 1930) is a British philosopher, appointed Emeritus Knightbridge Professor of Philosophy at Clare College, Cambridge University. He works primarily in philosophy of mathematics and logic. Life and career Timothy Smiley was born in London, the son of Professor M. T. Smiley and Mrs T. M. Smiley (née Browne). He was educated at Ardwyn Grammar School, Aberystwyth, followed by Ampleforth College, then went up to Clare College, Cambridge to read Mathematics in 1949. He obtained his BA degree in 1952 followed by a PhD in 1956 on natural systems of logic. After completing his PhD, he remained at Cambridge on a Research Fellowship at Clare (1955–59), then as a tutor and lecturer in philosophy. He also qualified as a pilot in the Air Ministry and was called to the bar at Gray's Inn. In 1980 he was appointed Knightbridge Professor of Philosophy, a post he held until his retirement in 1998. In 1982–83 he was President of the Aristotelian So ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
