|
Anderson Hamiltonian
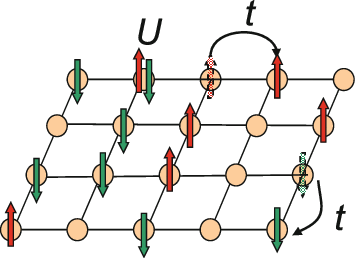
The Anderson impurity model, named after Philip Warren Anderson, is a Hamiltonian that is used to describe magnetic impurities embedded in metals. It is often applied to the description of Kondo effect-type problems, such as heavy fermion systems and Kondo insulators. In its simplest form, the model contains a term describing the kinetic energy of the conduction electrons, a two-level term with an on-site Coulomb repulsion that models the impurity energy levels, and a hybridization term that couples conduction and impurity orbitals. For a single impurity, the Hamiltonian takes the form :H = \sum_\epsilon_k c^_c_ + \sum_\epsilon_ d^_d_ + Ud^_d_d^_d_ + \sum_V_k(d^_c_ + c^_d_), where the c operator is the annihilation operator of a conduction electron, and d is the annihilation operator for the impurity, k is the conduction electron wavevector, and \sigma labels the spin. The on–site Coulomb repulsion is U, and V gives the hybridization. Regimes The model yields several re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Philip Warren Anderson
Philip Warren Anderson (December 13, 1923 – March 29, 2020) was an American theoretical physicist and Nobel laureate. Anderson made contributions to the theories of Anderson localization, localization, antiferromagnetism, symmetry breaking (including a paper in 1962 discussing symmetry breaking in particle physics, leading to the development of the Standard Model around 10 years later), and high-temperature superconductivity, and to the philosophy of science through his writings on emergent phenomena. Anderson is also responsible for naming the field of physics that is now known as condensed matter physics. Education and early life Anderson was born in Indianapolis, Indiana, and grew up in Urbana, Illinois. His father, Harry Warren Anderson, was a professor of plant pathology at the University of Illinois at Urbana–Champaign, University of Illinois at Urbana-Champaign; his maternal grandfather was a mathematician at Wabash College, where Anderson's father studied; and his m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Atomic Orbital
In quantum mechanics, an atomic orbital () is a Function (mathematics), function describing the location and Matter wave, wave-like behavior of an electron in an atom. This function describes an electron's Charge density, charge distribution around the Atomic nucleus, atom's nucleus, and can be used to calculate the probability of finding an electron in a specific region around the nucleus. Each orbital in an atom is characterized by a set of values of three quantum numbers , , and , which respectively correspond to electron's energy, its angular momentum, orbital angular momentum, and its orbital angular momentum projected along a chosen axis (magnetic quantum number). The orbitals with a well-defined magnetic quantum number are generally complex-valued. Real-valued orbitals can be formed as linear combinations of and orbitals, and are often labeled using associated Spherical harmonics#Harmonic polynomial representation, harmonic polynomials (e.g., ''xy'', ) which describe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Anderson Localization
In condensed matter physics, Anderson localization (also known as strong localization) is the absence of diffusion of waves in a ''disordered'' medium. This phenomenon is named after the American physicist P. W. Anderson, who was the first to suggest that electron localization is possible in a lattice potential, provided that the degree of randomness (disorder) in the lattice is sufficiently large, as can be realized for example in a semiconductor with impurities or defects. Anderson localization is a general wave phenomenon that applies to the transport of electromagnetic waves, acoustic waves, quantum waves, spin waves, etc. This phenomenon is to be distinguished from weak localization, which is the precursor effect of Anderson localization (see below), and from Mott localization, named after Sir Nevill Mott, where the transition from metallic to insulating behaviour is ''not'' due to disorder, but to a strong mutual Coulomb repulsion of electrons. Introduction In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kondo Model
The Kondo model (sometimes referred to as the s-d model) is a model for a single localized quantum impurity coupled to a large reservoir of delocalized and noninteracting electrons. The quantum impurity is represented by a spin-1/2 particle, and is coupled to a continuous band of noninteracting electrons by an antiferromagnetic exchange coupling J. The Kondo model is used as a model for metals containing magnetic impurities, as well as quantum dot systems. Kondo Hamiltonian The Kondo Hamiltonian is given by :H = \sum_ \epsilon_ c^_c_ - J \mathbf\cdot \mathbf where \mathbf is the spin-1/2 operator representing the impurity, and :\mathbf = \sum_ c^_ \mathbf_c_ is the local spin-density of the noninteracting band at the impurity site ( \mathbf are the Pauli matrices). In the Kondo problem, J 0). The Kondo model is intimately related to the Anderson impurity model, as can be shown by Schrieffer–Wolff transformation. See also * Anderson impurity model *Kondo effect In phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hubbard Model
The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard (physicist), John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian (quantum mechanics), Hamiltonian thus has two terms: a kinetic term allowing for Quantum tunneling, tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Number Operator
In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles. The following is in bra–ket notation: The number operator acts on Fock space. Let , \Psi\rangle_\nu=, \phi_1,\phi_2,\cdots,\phi_n\rangle_\nu be a Fock state, composed of single-particle states , \phi_i\rangle drawn from a basis of the underlying Hilbert space of the Fock space. Given the corresponding creation and annihilation operators a^(\phi_i) and a(\phi_i)\, we define the number operator by \hat \ \stackrel\ a^(\phi_i)a(\phi_i) and we have \hat, \Psi\rangle_\nu=N_i, \Psi\rangle_\nu where N_i is the number of particles in state , \phi_i\rangle. The above equality can be proven by noting that \begin a(\phi_i) , \phi_1,\phi_2,\cdots,\phi_,\phi_i,\phi_,\cdots,\phi_n\rangle_\nu &=& \sqrt , \phi_1,\phi_2,\cdots,\phi_,\phi_,\cdots,\phi_n\rangle_\nu \\ a^(\phi_i) , \phi_1,\phi_2,\cdots,\phi_,\phi_,\cdots,\phi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Carbon Nanotube Quantum Dot
A carbon nanotube quantum dot (CNT QD) is a small region of a carbon nanotube in which electrons are confined. Formation A CNT QD is formed when electrons are confined to a small region within a carbon nanotube. This is normally accomplished by application of a voltage to a gate electrode, dragging the valence band of the CNT down in energy, thereby causing electrons to pool in a region in the vicinity of the electrode. Experimentally this is accomplished by laying a CNT on a silicon dioxide surface, sitting on a doped silicon wafer. This can be done by chemical vapor deposition using carbon monoxide. The silicon wafer serves as the gate electrode. Metallic leads can then be laid over the nanotube in order to connect the CNT QD up to an electrical circuit. Electronic structure The CNT QD has interesting properties as a result of the strong correlation between the confined electrons. In addition to this the electrons possess orbital angular momentum, as is characteristic of C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Special Unitary Group
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1. The matrices of the more general unitary group may have complex determinants with absolute value 1, rather than real 1 in the special case. The group operation is matrix multiplication. The special unitary group is a normal subgroup of the unitary group , consisting of all unitary matrices. As a compact classical group, is the group that preserves the standard inner product on \mathbb^n. It is itself a subgroup of the general linear group, \operatorname(n) \subset \operatorname(n) \subset \operatorname(n, \mathbb ). The groups find wide application in the Standard Model of particle physics, especially in the electroweak interaction and in quantum chromodynamics. The simplest case, , is the trivial group, having only a single element. The group is isomorphic to the group of quaternions of norm 1, and is thus diffeomorphic to the 3-sphere. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hill Limit (solid-state)
In solid-state physics, the Hill limit is a critical distance defined in a lattice of actinide or rare-earth atoms. These atoms own partially filled 4f or 5f levels in their valence shell and are therefore responsible for the main interaction between each atom and its environment. In this context, the hill limit r_H is defined as twice the radius of the f-orbital. Therefore, if two atoms of the lattice are separate by a distance greater than the Hill limit, the overlap of their f-orbital becomes negligible. A direct consequence is the absence of hopping for the f electrons, ie their localization on the ion sites of the lattice. Localized f electrons lead to paramagnetic materials since the remaining unpaired spins are stuck in their orbitals. However, when the rare-earth lattice (or a single atom) is embedded in a metallic one (intermetallic compound An intermetallic (also called intermetallic compound, intermetallic alloy, ordered intermetallic alloy, long-range-ordered alloy) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fermi Level
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by ''μ'' or ''E''F for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics. In band structure theory, used in solid state physics to analyze the energy levels in a solid, the Fermi level can be considered to be a hypothetical energy level of an electron, such that at thermodynamic equilibrium this energy level would have a ''50% probability of being occupied at any given time''. The position of the Fermi level in relation to the band energy levels is a crucial factor in determining electrical properties. The Fer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hamiltonian (quantum Mechanics)
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's ''energy spectrum'' or its set of ''energy eigenvalues'', is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory. The Hamiltonian is named after William Rowan Hamilton, who developed a revolutionary reformulation of Newtonian mechanics, known as Hamiltonian mechanics, which was historically important to the development of quantum physics. Similar to vector notation, it is typically denoted by \hat, where the hat indicates that it is an operator. It can also be written as H or \check. Introduction The Hamiltonian of a system represents the total energy of the system; that is, the sum of the kine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spin (physics)
Spin is an Intrinsic and extrinsic properties, intrinsic form of angular momentum carried by elementary particles, and thus by List of particles#Composite particles, composite particles such as hadrons, atomic nucleus, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The relativistic spin–statistics theorem connects electron spin quantization to the Pauli exclusion principle: observations of exclusion imply half-integer spin, and observations of half-integer spin imply exclusion. Spin is described mathematically as a vector for some particles such as photons, and as a spinor or bispinor for other particles such as electrons. Sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |