|
Anderson's Rule
Anderson's rule is used for the construction of energy band diagrams of the heterojunction between two semiconductor materials. Anderson's rule states that when constructing an energy band diagram, the vacuum levels of the two semiconductors on either side of the heterojunction should be aligned (at the same energy). It is also referred to as the electron affinity rule, and is closely related to the Schottky–Mott rule for metal–semiconductor junctions. Anderson's rule was first described by R. L. Anderson in 1960. Constructing energy band diagrams Once the vacuum levels are aligned it is possible to use the electron affinity and band gap values for each semiconductor to calculate the conduction band and valence band offsets. The electron affinity (usually given by the symbol \chi in solid state physics) gives the energy difference between the lower edge of the conduction band and the vacuum level of the semiconductor. The band gap (usually given the symbol E_) gives the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heterojunction Variables In Equilibrium
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in many solid-state device applications, including semiconductor lasers, solar cells and transistors. The combination of multiple heterojunctions together in a device is called a heterostructure, although the two terms are commonly used interchangeably. The requirement that each material be a semiconductor with unequal band gaps is somewhat loose, especially on small length scales, where electronic properties depend on spatial properties. A more modern definition of heterojunction is the interface between any two solid-state materials, including crystalline and amorphous structures of metallic, insulating, fast ion conductor and semiconducting materials. Manufacture and applications Heterojunction manufacturing generally requires the use of mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Valence Band
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature, while the conduction band is the lowest range of vacant electronic states. On a graph of the electronic band structure of a material, the valence band is located below the Fermi level, while the conduction band is located above it. The distinction between the valence and conduction bands is meaningless in metals, because conduction occurs in one or more partially filled bands that take on the properties of both the valence and conduction bands. Band gap In semiconductors and insulators the two bands are separated by a band gap, while in semimetals the bands overlap. A band gap is an energy range in a solid where no electron states can exist due to the quantization of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiconductor Structures
A semiconductor is a material which has an electrical conductivity value falling between that of a conductor, such as copper, and an insulator, such as glass. Its resistivity falls as its temperature rises; metals behave in the opposite way. Its conducting properties may be altered in useful ways by introducing impurities (" doping") into the crystal structure. When two differently doped regions exist in the same crystal, a semiconductor junction is created. The behavior of charge carriers, which include electrons, ions, and electron holes, at these junctions is the basis of diodes, transistors, and most modern electronics. Some examples of semiconductors are silicon, germanium, gallium arsenide, and elements near the so-called " metalloid staircase" on the periodic table. After silicon, gallium arsenide is the second-most common semiconductor and is used in laser diodes, solar cells, microwave-frequency integrated circuits, and others. Silicon is a critical element for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
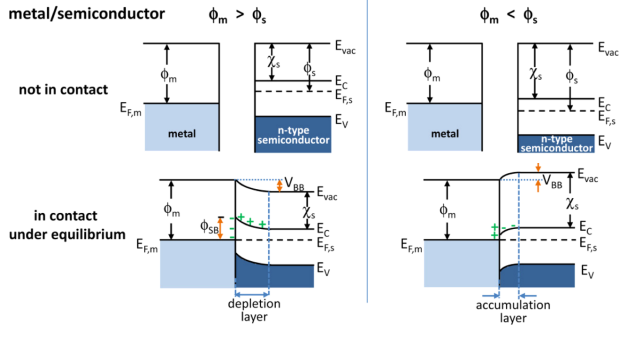
Metal-induced Gap States
In bulk semiconductor band structure calculations, it is assumed that the crystal lattice (which features a periodic potential due to the atomic structure) of the material is infinite. When the finite size of a crystal is taken into account, the wavefunctions of electrons are altered and states that are forbidden within the bulk semiconductor gap are allowed at the surface. Similarly, when a metal is deposited onto a semiconductor (by thermal evaporation, for example), the wavefunction of an electron in the semiconductor must match that of an electron in the metal at the interface. Since the Fermi levels of the two materials must match at the interface, there exists gap states that decay deeper into the semiconductor. Band-bending at the metal-semiconductor interface As mentioned above, when a metal is deposited onto a semiconductor, even when the metal film as small as a single atomic layer, the Fermi levels of the metal and semiconductor must match. This pins the Fermi level ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dipole
In physics, a dipole () is an electromagnetic phenomenon which occurs in two ways: *An electric dipole deals with the separation of the positive and negative electric charges found in any electromagnetic system. A simple example of this system is a pair of charges of equal magnitude but opposite sign separated by some typically small distance. (A permanent electric dipole is called an electret.) *A magnetic dipole is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet is an example of a magnet with a permanent magnetic dipole moment. Dipoles, whether electric or magnetic, can be characterized by their dipole moment, a vector quantity. For the simple electric dipole, the electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polarization Density
In classical electromagnetism, polarization density (or electric polarization, or simply polarization) is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is said to be polarized. The electric dipole moment induced per unit volume of the dielectric material is called the electric polarization of the dielectric.''Introduction to Electrodynamics'' (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ''McGraw Hill Encyclopaedia of Physics'' (2nd Edition), C.B. Parker, 1994, Polarization density also describes how a material responds to an applied electric field as well as the way the material changes the electric field, and can be used to calculate the forces that result from those interactions. It can be compared to magnetization, which is the measure of the corresponding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bonding
A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules and crystals. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing of electrons as in covalent bonds. The strength of chemical bonds varies considerably; there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force and hydrogen bonding. Strong chemical bonding arises from the sharing or transfer of electrons between the participating atoms. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. An electron positioned between two nuclei will be attracted to both of them, and the nuclei will be attracted toward electrons in this position. This attraction constitutes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band Bending
In solid-state physics, band bending refers to the process in which the electronic band structure in a material curves up or down near a junction or interface. It does not involve any physical (spatial) bending. When the electrochemical potential of the free charge carriers around an interface of a semiconductor is dissimilar, charge carriers are transferred between the two materials until an equilibrium state is reached whereby the potential difference vanishes. The band bending concept was first developed in 1938 when Mott, Davidov and Schottky all published theories of the rectifying effect of metal-semiconductor contacts. The use of semiconductor junctions sparked the computer revolution in 1990. Devices such as the diode, the transistor, the photocell and many more still play an important role in technology. Qualitative description Band bending can be induced by several types of contact. In this section metal-semiconductor contact, surface state, applied bias and adsorption ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson’s Equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson. Statement of the equation Poisson's equation is \Delta\varphi = f where \Delta is the Laplace operator, and f and \varphi are real or complex-valued functions on a manifold. Usually, f is given and \varphi is sought. When the manifold is Euclidean space, the Laplace operator is often denoted as and so Poisson's equation is frequently written as \nabla^2 \varphi = f. In three-dimensional Cartesian coordinates, it takes the form \left( \frac + \frac + \frac \right)\varp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band Offset
Band offset describes the relative alignment of the energy bands at a semiconductor heterojunction. Introduction At semiconductor heterojunctions, energy bands of two different materials come together, leading to an interaction. Both band structures are positioned discontinuously from each other, causing them to align close to the interface. This is done to ensure that the Fermi energy level stays continuous throughout the two semiconductors. This alignment is caused by the discontinuous band structures of the semiconductors when compared to each other and the interaction of the two surfaces at the interface. This relative alignment of the energy bands at such semiconductor heterojunctions is called the Band offset. The band offsets can be determined by both intrinsic properties, that is, determined by properties of the bulk materials, as well as non-intrinsic properties, namely, specific properties of the interface. Depending on the type of the interface, the offsets can be very ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vegard's Law
In crystallography, materials science and metallurgy, Vegard's law is an empirical finding (heuristic approach) resembling the rule of mixtures. In 1921, Lars Vegard discovered that the lattice parameter of a solid solution of two constituents is approximately a weighted mean of the two constituents' lattice parameters at the same temperature: :a_ = (1-x)\ a_\mathrm + x\ a_\mathrm e.g., in the case of a mixed oxide of uranium and plutonium as used in the fabrication of MOX nuclear fuel: :a_\mathrm = 0.93\ a_\mathrm + 0.07\ a_\mathrm Vegard's law assumes that both components A and B in their pure form (i.e. before mixing) have the same crystal structure. Here, is the lattice parameter of the solid solution, and are the lattice parameters of the pure constituents, and is the molar fraction of B in the solid solution. Vegard's law is seldom perfectly obeyed; often deviations from the linear behavior are observed. A detailed study of such deviations was conducted by King. Howe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alloys
An alloy is a mixture of chemical elements of which at least one is a metal. Unlike chemical compounds with metallic bases, an alloy will retain all the properties of a metal in the resulting material, such as electrical conductivity, ductility, opacity, and luster, but may have properties that differ from those of the pure metals, such as increased strength or hardness. In some cases, an alloy may reduce the overall cost of the material while preserving important properties. In other cases, the mixture imparts synergistic properties to the constituent metal elements such as corrosion resistance or mechanical strength. Alloys are defined by a metallic bonding character. The alloy constituents are usually measured by mass percentage for practical applications, and in atomic fraction for basic science studies. Alloys are usually classified as substitutional or interstitial alloys, depending on the atomic arrangement that forms the alloy. They can be further classified as homogene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |