|
Algebra Bundle
In mathematics, an algebra bundle is a fiber bundle whose fibers are algebras and local trivializations respect the algebra structure. It follows that the transition functions are algebra isomorphisms. Since algebras are also vector spaces, every algebra bundle is a vector bundle. Examples include the tensor-algebra bundle, exterior bundle, and symmetric bundle associated to a given vector bundle, as well as the Clifford bundle In mathematics, a Clifford bundle is an algebra bundle whose fibers have the structure of a Clifford algebra and whose local trivializations respect the algebra structure. There is a natural Clifford bundle associated to any (pseudo) Riemannian ... associated to any Riemannian vector bundle. See also * Lie algebra bundle References *. *. *. *. Vector bundles {{algebra-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
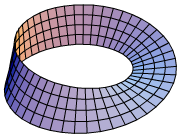
Fiber Bundle
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a product space B \times F is defined using a continuous surjective map, \pi : E \to B, that in small regions of E behaves just like a projection from corresponding regions of B \times F to B. The map \pi, called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space E is known as the total space of the fiber bundle, B as the base space, and F the fiber. In the ''trivial'' case, E is just B \times F, and the map \pi is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces. Fiber bundles, such as the tangent bundle of a man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiber (mathematics)
In mathematics, the term fiber (US English) or fibre (British English) can have two meanings, depending on the context: # In naive set theory, the fiber of the element y in the set Y under a map f : X \to Y is the inverse image of the singleton \ under f. # In algebraic geometry, the notion of a fiber of a morphism of schemes must be defined more carefully because, in general, not every point is closed. Definitions Fiber in naive set theory Let f : X \to Y be a function between sets. The fiber of an element y \in Y (or ''fiber over'' y) under the map f is the set f^(y) = \, that is, the set of elements that get mapped to y by the function. It is the preimage of the singleton \. (One usually takes y in the image of f to avoid f^(y) being the empty set.) The collection of all fibers for the function f forms a partition of the domain X. The fiber containing an element x\in X is the set f^(f(x)). For example, the fibers of the projection map \R^2\to\R that sends (x,y) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Over A Field
In mathematics, an algebra over a field (often simply called an algebra) is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition and scalar multiplication by elements of a field and satisfying the axioms implied by "vector space" and "bilinear". The multiplication operation in an algebra may or may not be associative, leading to the notions of associative algebras and non-associative algebras. Given an integer ''n'', the ring of real square matrices of order ''n'' is an example of an associative algebra over the field of real numbers under matrix addition and matrix multiplication since matrix multiplication is associative. Three-dimensional Euclidean space with multiplication given by the vector cross product is an example of a nonassociative algebra over the field of real numbers since the vector cross product is nonassociative, satisfying the Jacobi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Trivialization
In mathematics, and particularly topology, a fiber bundle (or, in Commonwealth English: fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a product space B \times F is defined using a continuous surjective map, \pi : E \to B, that in small regions of E behaves just like a projection from corresponding regions of B \times F to B. The map \pi, called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space E is known as the total space of the fiber bundle, B as the base space, and F the fiber. In the ''trivial'' case, E is just B \times F, and the map \pi is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces. Fiber bundles, such as the tangent bundle of a manifo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Map
In mathematics, particularly topology, one describes a manifold using an atlas. An atlas consists of individual ''charts'' that, roughly speaking, describe individual regions of the manifold. If the manifold is the surface of the Earth, then an atlas has its more common meaning. In general, the notion of atlas underlies the formal definition of a manifold and related structures such as vector bundles and other fiber bundles. Charts The definition of an atlas depends on the notion of a ''chart''. A chart for a topological space ''M'' (also called a coordinate chart, coordinate patch, coordinate map, or local frame) is a homeomorphism \varphi from an open subset ''U'' of ''M'' to an open subset of a Euclidean space. The chart is traditionally recorded as the ordered pair (U, \varphi). Formal definition of atlas An atlas for a topological space M is an indexed family \ of charts on M which covers M (that is, \bigcup_ U_ = M). If the codomain of each chart is the ''n''-dimensional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Isomorphism
In mathematics, an algebra homomorphism is a homomorphism between two associative algebras. More precisely, if and are algebras over a field (or commutative ring) , it is a function F\colon A\to B such that for all in and in , * F(kx) = kF(x) * F(x + y) = F(x) + F(y) * F(xy) = F(x) F(y) The first two conditions say that is a ''K''-linear map (or ''K''-module homomorphism if ''K'' is a commutative ring), and the last condition says that is a (non-unital) ring homomorphism. If admits an inverse homomorphism, or equivalently if it is bijective, is said to be an isomorphism between and . Unital algebra homomorphisms If ''A'' and ''B'' are two unital algebras, then an algebra homomorphism F:A\rightarrow B is said to be ''unital'' if it maps the unity of ''A'' to the unity of ''B''. Often the words "algebra homomorphism" are actually used to mean "unital algebra homomorphism", in which case non-unital algebra homomorphisms are excluded. A unital algebra homomorphism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called '' vectors'', may be added together and multiplied ("scaled") by numbers called ''scalars''. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space. Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a manifold ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor-algebra Bundle
In mathematics, the tensor algebra of a vector space ''V'', denoted ''T''(''V'') or ''T''(''V''), is the algebra of tensors on ''V'' (of any rank) with multiplication being the tensor product. It is the free algebra on ''V'', in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing ''V'', in the sense of the corresponding universal property (see below). The tensor algebra is important because many other algebras arise as quotient algebras of ''T''(''V''). These include the exterior algebra, the symmetric algebra, Clifford algebras, the Weyl algebra and universal enveloping algebras. The tensor algebra also has two coalgebra structures; one simple one, which does not make it a bialgebra, but does lead to the concept of a cofree coalgebra, and a more complicated one, which yields a bialgebra, and can be extended by giving an antipode to create a Hopf algebra structure. ''Note'': In this article, all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exterior Bundle
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps (e.g. multiplication) to be carried out in terms of linear maps. The module construction is analogous to the construction of the tensor product of vector spaces, but can be carried out for a pair of modules over a commutative ring resulting in a third module, and also for a pair of a right-module and a left-module over any ring, with result an abelian group. Tensor products are important in areas of abstract algebra, homological algebra, algebraic topology, algebraic geometry, operator algebras and noncommutative geometry. The universal property of the tensor product of vector spaces extends to more general situations in abstract algebra. It allows the study of bilinear or multilinear operations via linear operations. The tensor product of an algebra and a module can be used for extension of scalars. For a commutative ring, the tensor product of modules can be iterated to fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Bundle
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |