|
ALGLIB
ALGLIB is a cross-platform open source numerical analysis and data processing library. It can be used from several programming languages ( C++, C#, VB.NET, Python, Delphi, Java). ALGLIB started in 1999 and has a long history of steady development with roughly 1-3 releases per year. It is used by several open-source projects, commercial libraries, and applications (e.g. TOL project, Math.NET Numerics, SpaceClaim). Features Distinctive features of the library are: * Support for several programming languages with identical APIs (as of 2023, it supports C++, C#, FreePascal/Delphi, VB.NET, Python, and Java) * Self-contained code with no mandatory external dependencies and easy installation * Portability (it was tested under x86/x86-64/ARM, Windows and Linux) * Two independent backends (pure C# implementation, native C implementation) with automatically generated APIs (C++, C#, ...) * Same functionality of commercial and GPL versions, with enhancements for speed and parallelism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Numerical Libraries
This is a list of numerical libraries, which are libraries used in software development for performing numerical calculations. It is not a complete listing but is instead a list of numerical libraries with articles on Wikipedia, with few exceptions. The choice of a typical library depends on a range of requirements such as: desired features (e.g. large dimensional linear algebra, parallel computation, partial differential equations), licensing, readability of API, portability or platform/compiler dependence (e.g. Linux, Windows, Visual C++, GCC), performance, ease-of-use, continued support from developers, standard compliance, specialized optimization in code for specific application scenarios or even the size of the code-base to be installed. Multi-language C C++ Delphi * ALGLIB - an open source numerical analysis library. .NET Framework languages C#, F#, VB.NET and PowerShell Fortran Java OCaml * OCaml programming language has support for array programming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Fourier Transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by Matrix decomposition, factorizing the DFT matrix into a product of Sparse matrix, sparse (mostly zero) factors. As a result, it manages to reduce the Computational complexity theory, complexity of computing the DFT from O(n^2), which arises if one simply applies the definition of DFT, to O(n \log n), where is the data size. The difference in speed can be enormous, especially for long data sets where may be in the thousands or millions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MPFR
The GNU Multiple Precision Floating-Point Reliable Library (GNU MPFR) is a GNU portable C (programming language), C Library (computing), library for Arbitrary-precision arithmetic, arbitrary-precision binary Floating-point arithmetic, floating-point computation with rounding#Table-maker's dilemma, correct rounding, based on GNU Multiple Precision Arithmetic Library, GNU Multi-Precision Library. Library MPFR's computation is both efficient and has a well-defined semantics: the functions are completely specified on all the possible operands and the results do not depend on the platform. This is done by copying the ideas from the IEEE 754, ANSI/IEEE-754 standard for fixed-precision floating-point arithmetic (correct rounding and exceptions, in particular). More precisely, its main features are: * Support for special numbers: signed zeros (+0 and −0), Infinity#Computing, infinities and NaN, not-a-number (a single NaN is supported: MPFR does not differentiate between quiet NaNs and s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross-platform
Within computing, cross-platform software (also called multi-platform software, platform-agnostic software, or platform-independent software) is computer software that is designed to work in several Computing platform, computing platforms. Some cross-platform software requires a separate build for each platform, but some can be directly run on any platform without special preparation, being written in an interpreted language or compiled to portable bytecode for which the Interpreter (computing), interpreters or run-time packages are common or standard components of all supported platforms. For example, a cross-platform application software, application may run on Linux, macOS and Microsoft Windows. Cross-platform software may run on many platforms, or as few as two. Some frameworks for cross-platform development are Codename One, ArkUI-X, Kivy (framework), Kivy, Qt (software), Qt, GTK, Flutter (software), Flutter, NativeScript, Xamarin, Apache Cordova, Ionic (mobile app framework ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linux
Linux ( ) is a family of open source Unix-like operating systems based on the Linux kernel, an kernel (operating system), operating system kernel first released on September 17, 1991, by Linus Torvalds. Linux is typically package manager, packaged as a Linux distribution (distro), which includes the kernel and supporting system software and library (computing), libraries—most of which are provided by third parties—to create a complete operating system, designed as a clone of Unix and released under the copyleft GPL license. List of Linux distributions, Thousands of Linux distributions exist, many based directly or indirectly on other distributions; popular Linux distributions include Debian, Fedora Linux, Linux Mint, Arch Linux, and Ubuntu, while commercial distributions include Red Hat Enterprise Linux, SUSE Linux Enterprise, and ChromeOS. Linux distributions are frequently used in server platforms. Many Linux distributions use the word "Linux" in their name, but the Free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
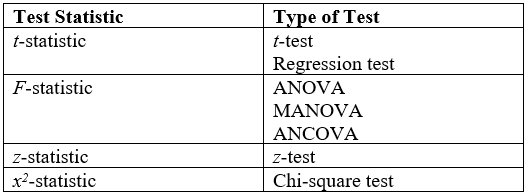
Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe test of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descriptive Statistics
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics (in the mass noun sense) is the process of using and analysing those statistics. Descriptive statistics is distinguished from inferential statistics (or inductive statistics) by its aim to summarize a sample, rather than use the data to learn about the population that the sample of data is thought to represent. This generally means that descriptive statistics, unlike inferential statistics, is not developed on the basis of probability theory, and are frequently nonparametric statistics. Even when a data analysis draws its main conclusions using inferential statistics, descriptive statistics are generally also presented. For example, in papers reporting on human subjects, typically a table is included giving the overall sample size, sample sizes in important subgroups (e.g., for each treatmen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Functions
Special functions are particular mathematical functions that have more or less established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other applications. The term is defined by consensus, and thus lacks a general formal definition, but the list of mathematical functions contains functions that are commonly accepted as special. Tables of special functions Many special functions appear as solutions of differential equations or integrals of elementary functions. Therefore, tables of integrals usually include descriptions of special functions, and tables of special functions include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie groups and Lie algebras, as well as certain topics in mathematical physics. Symbolic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable (mathematics), variable. As with any other DE, its unknown(s) consists of one (or more) Function (mathematics), function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equation, ''partial'' differential equations (PDEs) which may be with respect to one independent variable, and, less commonly, in contrast with stochastic differential equations, ''stochastic'' differential equations (SDEs) where the progression is random. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where a_0(x),\ldots,a_n(x) and b(x) are arbitrary differentiable functions that do not need to be linea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |