|
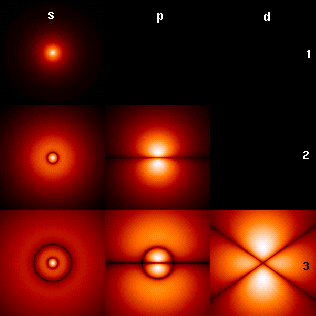
Azimuthal Quantum Number
In quantum mechanics, the azimuthal quantum number is a quantum number for an atomic orbital that determines its angular momentum operator, orbital angular momentum and describes aspects of the angular shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron (the others being the principal quantum number , the magnetic quantum number , and the spin quantum number ). For a given value of the principal quantum number (''electron shell''), the possible values of are the integers from 0 to . For instance, the shell has only orbitals with \ell=0, and the shell has only orbitals with \ell=0, and \ell=1. For a given value of the azimuthal quantum number , the possible values of the magnetic quantum number are the integers from to , including 0. In addition, the spin quantum number can take two distinct values. The set of orbitals associated with a particular value of are som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spherical Coordinate System
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are * the radial distance along the line connecting the point to a fixed point called the origin; * the polar angle between this radial line and a given ''polar axis''; and * the azimuthal angle , which is the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (''r'', ''θ'', ''φ''), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the ''reference plane'' (sometimes '' fundamental plane''). Terminology The radial distance from the fixed point of origin is also called the ''radius'', or ''radial line'', or ''radial coor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Block (periodic Table)
A block of the periodic table is a set of elements unified by the atomic orbitals their valence electrons or vacancies lie in. The term seems to have been first used by Charles Janet. Each block is named after its characteristic orbital: s-block, p-block, d-block, f-block and g-block. The block names (s, p, d, and f) are derived from the spectroscopic notation for the value of an electron's azimuthal quantum number: sharp (0), principal (1), diffuse (2), and fundamental (3). Succeeding notations proceed in alphabetical order, as g, h, etc., though elements that would belong in such blocks have not yet been found. Characteristics There is an ''approximate'' correspondence between this nomenclature of blocks, based on electronic configuration, and sets of elements based on chemical properties. The s-block and p-block together are usually considered main-group elements, the d-block corresponds to the transition metals, and the f-block corresponds to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Energy Level Splitting
In quantum physics, energy level splitting or a split in an energy level of a quantum system occurs when a perturbation changes the system. The perturbation changes the corresponding Hamiltonian and the outcome is change in eigenvalues; several distinct energy levels emerge in place of the former degenerate (multi-state) level. This may occur because of external fields, quantum tunnelling between states, or other effects. The term is most commonly used in reference to the electron configuration in atoms or molecules. The simplest case of level splitting is a quantum system with two states whose unperturbed Hamiltonian is a diagonal operator: , where is the identity matrix. Eigenstates and eigenvalues (energy levels) of a perturbed Hamiltonian :\hat H_\varepsilon = \hat H_0+\varepsilon\sigma_3 =\begin E_0+\varepsilon & 0 \\ 0 & E_0-\varepsilon \end will be: : : the level, and : : the level, so this degenerate eigenvalue splits in two whenever . Though, if a perturbed Ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Energy Level
A quantum mechanics, quantum mechanical system or particle that is bound state, bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical mechanics, classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the atomic nucleus, nucleus, but can also refer to energy levels of nuclei or molecular vibration, vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be Quantization (physics), quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's atomic nucleus, nucleus. The closest shell to the nucleus is called the "1 shell" (also called "K shell"), followed by the "2 shell" (or "L shell"), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hydrogen-like Atom
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars. The non-relativistic Schrödinger equation and relativistic Dirac equation for the hydrogen atom can be solved analytically, owing to the simplicity of the two-particle physical system. The one-electron wave function solutions are referred to as ''hydrogen-like atomic orbitals''. Hydrogen-li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Angular Momentum Quantization
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Being an observable, its eigenfunctions represent the distinguishable physical states of a system's angular momentum, and the corresponding eigenvalues the observable experimental values. When applied to a mathematical representation of the state of a system, yields the same state multiplied by its angular momentum value if the state is an eigenstate (as per the eigenstates/eigenvalues equation). In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is one of the three fundamental properties of motion.Introductory Quantum Mechanics, Richard L. Liboff, 2nd Edition, There are several angular momentum operators: total angular momentum (usually denot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |