|
Archetypal Analysis
Archetypal analysis in statistics is an unsupervised learning method similar to cluster analysis and introduced by Adele Cutler and Leo Breiman Leo Breiman (January 27, 1928 – July 5, 2005) was a distinguished statistician at the University of California, Berkeley. He was the recipient of numerous honors and awards, and was a member of the United States National Academy of Sciences. ... in 1994. Rather than "typical" observations (cluster centers), it seeks extremal points in the multidimensional data, the " archetypes". The archetypes are convex combinations of observations chosen so that observations can be approximated by convex combinations of the archetypes. Literature * Adele Cutler and Leo Breiman. Archetypal analysis. Technometrics, 36(4):338–347, November 1994. Manuel J. A. Eugster: Archetypal Analysis, Mining the Extreme. HIIT seminar, Helsinki Institute for Information Technology, 2012* Anil Damle, Yuekai Sun: A geometric approach to archetypal analysis and no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unsupervised Learning
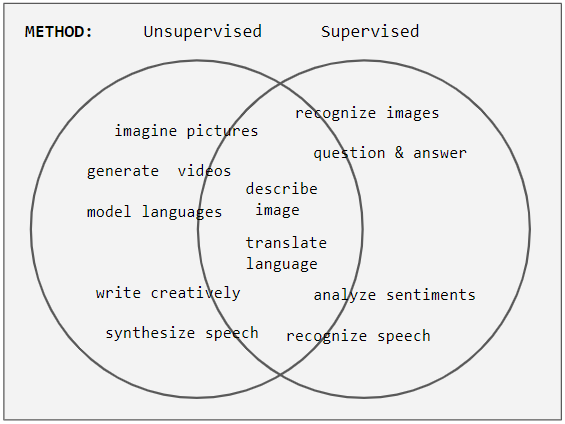
Unsupervised learning is a type of algorithm that learns patterns from untagged data. The hope is that through mimicry, which is an important mode of learning in people, the machine is forced to build a concise representation of its world and then generate imaginative content from it. In contrast to supervised learning where data is tagged by an expert, e.g. tagged as a "ball" or "fish", unsupervised methods exhibit self-organization that captures patterns as probability densities or a combination of neural feature preferences encoded in the machine's weights and activations. The other levels in the supervision spectrum are reinforcement learning where the machine is given only a numerical performance score as guidance, and semi-supervised learning where a small portion of the data is tagged. Neural networks Tasks vs. methods Neural network tasks are often categorized as discriminative (recognition) or generative (imagination). Often but not always, discriminative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cluster Analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis itself is not one specific algorithm, but the general task to be solved. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small distances between cluster members, dense areas of the data space, intervals or particular statistical distributions. Clustering can therefore be formulated as a multi-objective optimization probl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adele Cutler
Adele Cutler is a statistician known as one of the developers of archetypal analysis and of the random forest technique for ensemble learning. She is a professor of mathematics and statistics at Utah State University. Early life and education Originally from England, Cutler moved to New Zealand as a child, and studied mathematics at the University of Waikato and the University of Auckland. She met her husband, statistician Richard Cutler, at the University of Auckland; the couple both went on to graduate study in statistics at the University of California, Berkeley, where she earned a master's degree in 1984 and completed her doctorate in 1988. Her dissertation, ''Optimization Methods in Statistics'', was supervised by Leo Breiman. Her doctoral work with Breiman concerned mathematical optimization techniques in statistics, and introduced archetypal analysis. Career After completing her doctorate she joined the faculty at Utah State University in 1988. Her initial research ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leo Breiman
Leo Breiman (January 27, 1928 – July 5, 2005) was a distinguished statistician at the University of California, Berkeley. He was the recipient of numerous honors and awards, and was a member of the United States National Academy of Sciences. Breiman's work helped to bridge the gap between statistics and computer science, particularly in the field of machine learning. His most important contributions were his work on classification and regression trees and ensembles of trees fit to bootstrap samples. Bootstrap aggregation was given the name ''bagging'' by Breiman. Another of Breiman's ensemble approaches is the random forest Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of th .... See also * Shannon–McMillan–Breiman theorem Further reading * Leo Breimaobituary from t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archetype
The concept of an archetype (; ) appears in areas relating to behavior, historical psychology, and literary analysis. An archetype can be any of the following: # a statement, pattern of behavior, prototype, "first" form, or a main model that other statements, patterns of behavior, and objects copy, emulate, or "merge" into. Informal synonyms frequently used for this definition include "standard example", "basic example", and the longer-form "archetypal example"; mathematical archetypes often appear as " canonical examples". # the Platonic concept of ''pure form'', believed to embody the fundamental characteristics of a thing. # a collectively-inherited unconscious idea, a pattern of thought, image, etc., that is universally present, in individual psyches, as in Jungian psychology # a constantly-recurring symbol or motif in literature, painting, or mythology. This definition refers to the recurrence of characters or ideas sharing similar traits throughout various, seemingly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Combination
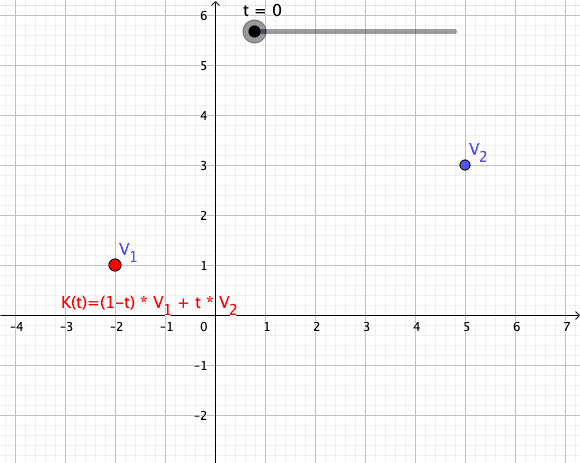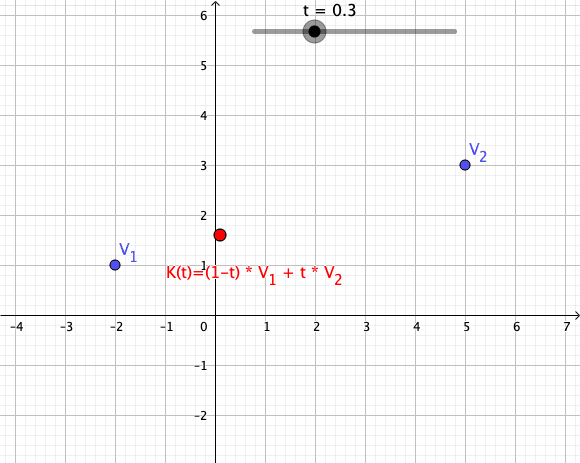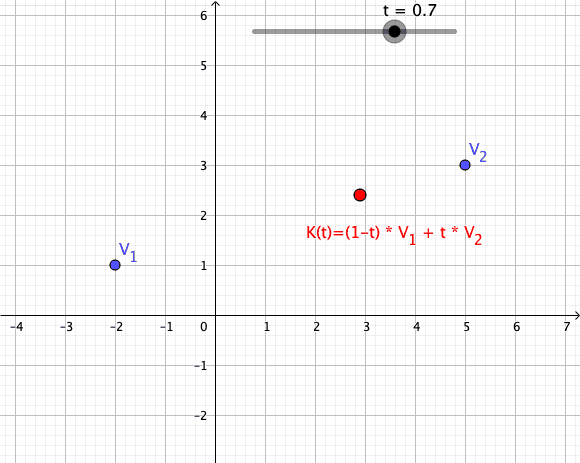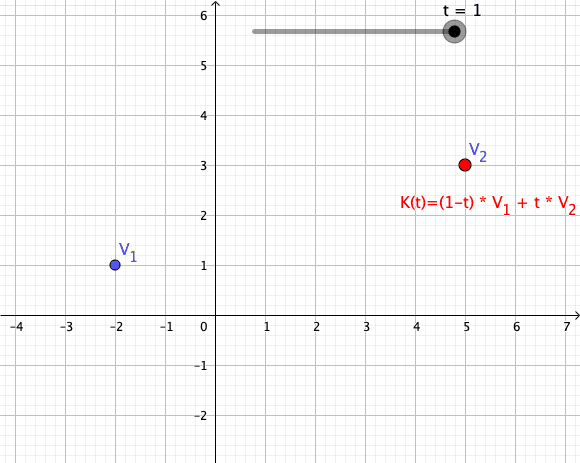
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is id ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |