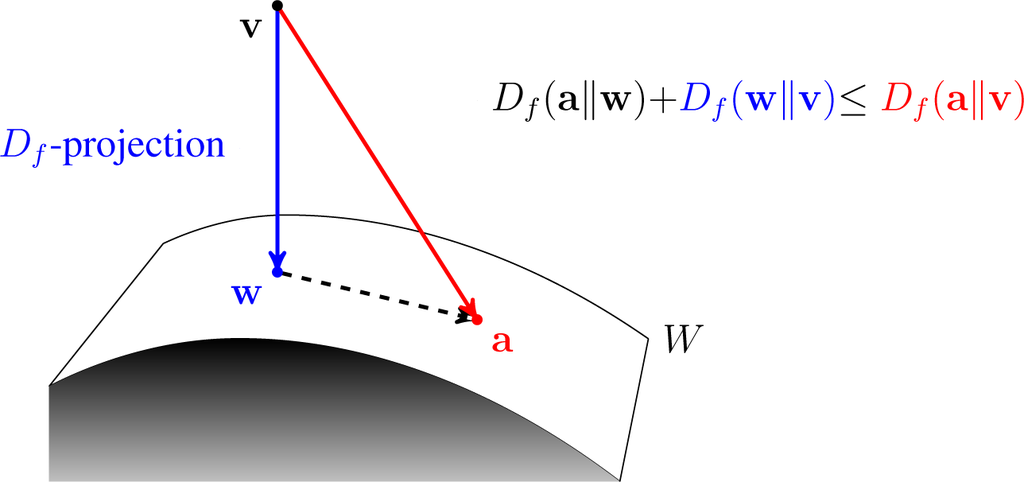
|
Approximate Inference
Approximate inference methods make it possible to learn realistic models from big data Though used sometimes loosely partly because of a lack of formal definition, the interpretation that seems to best describe Big data is the one associated with large body of information that we could not comprehend when used only in smaller am ... by trading off computation time for accuracy, when exact learning and inference are computationally intractable. Major methods classes *Laplace's approximation *Variational Bayesian methods *Markov chain Monte Carlo *Expectation propagation *Markov random fields *Bayesian networks **Variational message passing * Loopy and generalized belief propagation See also *Statistical inference *Fuzzy logic *Data mining References External links *{{cite web, url=http://videolectures.net/mlss09uk_minka_ai/, title=Machine Learning Summer School (MLSS), Cambridge 2009, Approximate Inference, author= Tom Minka, Microsoft Research, date=Nov 2, 2009, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big Data
Though used sometimes loosely partly because of a lack of formal definition, the interpretation that seems to best describe Big data is the one associated with large body of information that we could not comprehend when used only in smaller amounts. In it primary definition though, Big data refers to data sets that are too large or complex to be dealt with by traditional data-processing application software. Data with many fields (rows) offer greater statistical power, while data with higher complexity (more attributes or columns) may lead to a higher false discovery rate. Big data analysis challenges include capturing data, data storage, data analysis, search, sharing, transfer, visualization, querying, updating, information privacy, and data source. Big data was originally associated with three key concepts: ''volume'', ''variety'', and ''velocity''. The analysis of big data presents challenges in sampling, and thus previously allowing for only observations and sampling. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inference
Inferences are steps in reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in Europe dates at least to Aristotle (300s BCE). Deduction is inference deriving logical conclusions from premises known or assumed to be true, with the laws of valid inference being studied in logic. Induction is inference from particular evidence to a universal conclusion. A third type of inference is sometimes distinguished, notably by Charles Sanders Peirce, contradistinguishing abduction from induction. Various fields study how inference is done in practice. Human inference (i.e. how humans draw conclusions) is traditionally studied within the fields of logic, argumentation studies, and cognitive psychology; artificial intelligence researchers develop automated inference systems to emulate human inference. Statistical inference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computationally Intractable
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). One of the roles of computati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace's Approximation
In mathematics, Laplace's approximation fits an un-normalised Gaussian approximation to a (twice differentiable) un-normalised target density. In Bayesian statistical inference this is useful to simultaneously approximate the posterior and the marginal likelihood, see also Approximate inference. The method works by matching the log density and curvature at a mode of the target density. For example, a (possibly non-linear) regression or classification model with data set \_ comprising inputs x and outputs y has (unknown) parameter vector \theta of length D. The likelihood is denoted p(, ,\theta) and the parameter prior p(\theta). The joint density of outputs and parameters p(,\theta, ) is the object of inferential desire : p(,\theta, )\;=\;p(, ,\theta)p(\theta)\;=\;p(, )p(\theta, ,)\;\simeq\;\tilde q(\theta)\;=\;Zq(\theta). The joint is equal to the product of the likelihood and the prior and by Bayes' rule, equal to the product of the marginal likelihood p(, ) and posterio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Bayesian Method
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes: #To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables. #To derive a lower bound for the marginal likelihood (sometimes called the ''evidence'') of the observed data (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm. Application domains MCMC methods are primarily used for calculating numerical approximations of multi-dimensional integrals, for example in Bayesian statistics, computational physics, computational biology and computational linguistics. In Bayesian statistics, the recent development of MCMC methods has made it possible to compute large hierarchical models that require integrations over hundreds to thousands of unknown parameters. In rare even ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expectation Propagation
Expectation propagation (EP) is a technique in Bayesian machine learning. EP finds approximations to a probability distribution. It uses an iterative approach that uses the factorization structure of the target distribution. It differs from other Bayesian approximation approaches such as variational Bayesian methods. More specifically, suppose we wish to approximate an intractable probability distribution p(\mathbf) with a tractable distribution q(\mathbf). Expectation propagation achieves this approximation by minimizing the Kullback-Leibler divergence \mathrm(p, , q). Variational Bayesian methods minimize \mathrm(q, , p) instead. If q(\mathbf) is a Gaussian \mathcal(\mathbf, \mu, \Sigma), then \mathrm(p, , q) is minimized with \mu and \Sigma being equal to the mean of p(\mathbf) and the covariance of p(\mathbf), respectively; this is called moment matching. Applications Expectation propagation via moment matching plays a vital role in approximation for indicator functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Random Field
In the domain of physics and probability, a Markov random field (MRF), Markov network or undirected graphical model is a set of random variables having a Markov property described by an undirected graph. In other words, a random field is said to be a Markov random field if it satisfies Markov properties. The concept originates from the Sherrington–Kirkpatrick model. A Markov network or MRF is similar to a Bayesian network in its representation of dependencies; the differences being that Bayesian networks are directed and acyclic, whereas Markov networks are undirected and may be cyclic. Thus, a Markov network can represent certain dependencies that a Bayesian network cannot (such as cyclic dependencies ); on the other hand, it can't represent certain dependencies that a Bayesian network can (such as induced dependencies ). The underlying graph of a Markov random field may be finite or infinite. When the joint probability density of the random variables is strictly positive, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Network
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases. Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (''e.g.'' speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams. Graphical mode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Message Passing
Variational message passing (VMP) is an approximate inference technique for continuous- or discrete-valued Bayesian networks, with conjugate-exponential parents, developed by John Winn. VMP was developed as a means of generalizing the approximate variational methods used by such techniques as latent Dirichlet allocation, and works by updating an approximate distribution at each node through messages in the node's Markov blanket. Likelihood lower bound Given some set of hidden variables H and observed variables V, the goal of approximate inference is to lower-bound the probability that a graphical model is in the configuration V. Over some probability distribution Q (to be defined later), : \ln P(V) = \sum_H Q(H) \ln \frac = \sum_ Q(H) \Bigg \ln \frac - \ln \frac \Bigg . So, if we define our lower bound to be : L(Q) = \sum_ Q(H) \ln \frac , then the likelihood is simply this bound plus the relative entropy between P and Q. Because the relative entropy is non-negative, the funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Belief Propagation
A belief is an attitude that something is the case, or that some proposition is true. In epistemology, philosophers use the term "belief" to refer to attitudes about the world which can be either true or false. To believe something is to take it to be true; for instance, to believe that snow is white is comparable to accepting the truth of the proposition "snow is white". However, holding a belief does not require active introspection. For example, few carefully consider whether or not the sun will rise tomorrow, simply assuming that it will. Moreover, beliefs need not be ''occurrent'' (e.g. a person actively thinking "snow is white"), but can instead be ''dispositional'' (e.g. a person who if asked about the color of snow would assert "snow is white"). There are various different ways that contemporary philosophers have tried to describe beliefs, including as representations of ways that the world could be (Jerry Fodor), as dispositions to act as if certain things are true (Rod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Inference
Statistical inference is the process of using data analysis to infer properties of an underlying probability distribution, distribution of probability.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a Statistical population, population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is Sampling (statistics), sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
