|
19 Tone Equal Temperament
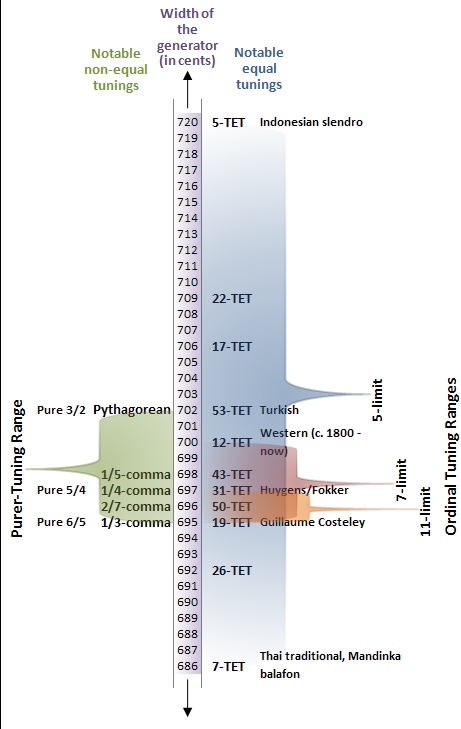
In music, 19 Tone Equal Temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 63.16 cents (). The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings. 19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12 EDO), so long as the notes are "spelled properly" – that is, with no assumption that the sharp below matches the flat immediately above it (enharmon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
31 Equal Temperament
In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET (31 tone ET) or 31- EDO (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps (equal frequency ratios). Each step represents a frequency ratio of , or 38.71 cents (). 31-ET is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in 31-ET is precisely the same as it is in any other syntonic tuning (such as 12-ET), so long as the notes are spelled properly — that is, with no assumption of enharmonicity. History and use Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis — the ratio of an octave to three major thirds, 128:125 or 41.06 cents — was approximat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Seventh
The harmonic seventh interval, also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio (about 969 cents). This is somewhat narrower than and is, "particularly sweet", "sweeter in quality" than an "ordinary" just minor seventh, which has an intonation ratio of 9:5 (about 1018 cents). The harmonic seventh arises from the harmonic series as the interval between the fourth harmonic (second octave of the fundamental) and the seventh harmonic; in that octave, harmonics 4, 5, 6, and 7 constitute a purely consonant major chord with added seventh (root position). When played on the natural horn, as a compromise the note is often adjusted to 16:9 of the root (for C maj7, the substituted note is B, 996.09 cents), but some pieces call for the pure harmonic seventh, including Britten's ''Serenade for Tenor, Horn and Strings''. Composer Ben Johnston uses a small "7" as an accidental to indicate a note is lowered 49 cents ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor Seventh
In music theory, a minor seventh is one of two musical intervals that span seven staff positions. It is ''minor'' because it is the smaller of the two sevenths, spanning ten semitones. The major seventh spans eleven. For example, the interval from A to G is a minor seventh, as the note G lies ten semitones above A, and there are seven staff positions from A to G. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones (nine and twelve, respectively). Minor seventh intervals rarely feature in melodies (and especially in their openings) but occur more often than major sevenths. The best-known example, in part due to its frequent use in theory classes, is found between the first two words of the phrase "There's a place for us" in the song " Somewhere" in ''West Side Story''.Neely, Blake (2009). ''Piano For Dummies'', p.201. . Another well-known example occurs between the first two notes of the introduction to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Seventh
In music from Western culture, a seventh is a musical interval encompassing seven staff positions (see Interval number for more details), and the major seventh is one of two commonly occurring sevenths. It is qualified as ''major'' because it is the larger of the two. The major seventh spans eleven semitones, its smaller counterpart being the minor seventh, spanning ten semitones. For example, the interval from C to B is a major seventh, as the note B lies eleven semitones above C, and there are seven staff positions from C to B. Diminished and augmented sevenths span the same number of staff positions, but consist of a different number of semitones (nine and twelve). The easiest way to locate and identify the major seventh is from the octave rather than the unison, and it is suggested that one sings the octave first.Keith Wyatt, Carl Schroeder, Joe Elliott (2005). ''Ear Training for the Contemporary Musician'', p.69. . For example, the most commonly cited example of a melod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diminished Octave
In music from Western culture, a diminished octave () is an interval produced by narrowing a perfect octave by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . Specific example of an d8 not given but general example of perfect intervals described. As such, the two notes are denoted by the same letter but have different accidentals. For instance, the interval from C4 to C5 is a perfect octave, twelve semitones wide, and both the intervals from C4 to C5 and from C4 to C5 are diminished octaves, spanning eleven semitones. Being diminished, it is considered a dissonant interval.Benward & Saker (2003), p.92. The diminished octave is enharmonically equivalent to the major seventh In music from Western culture, a seventh is a musical interval encompassing seven staff positions (see Interval number for more details), and the major seventh is one of two commonly occurring sevenths. It is qualified as ''major'' because it i .... Refere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music," the use of which is "common in most musical systems." The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' ( it, all'ottava), ''8va bassa'' ( it, all'ottava bassa, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12 Equal Temperament
Twelve-tone equal temperament (12-TET) is the musical system that divides the octave into 12 parts, all of which are equally tempered (equally spaced) on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resulting smallest interval, the width of an octave, is called a semitone or half step. Twelve-tone equal temperament is the most widespread system in music today. It has been the predominant tuning system of Western music, starting with classical music, since the 18th century, and Europe almost exclusively used approximations of it for millennia before that. It has also been used in other cultures. In modern times, 12-TET is usually tuned relative to a standard pitch of 440 Hz, called A440, meaning one note, A, is tuned to 440 hertz and all other notes are defined as some multiple of semitones apart from it, either higher or lower in frequency. The standard pitch has not always been 440 Hz. It has varied and generally risen over t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series (music)
A harmonic series (also overtone series) is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a ''fundamental frequency''. Pitched musical instruments are often based on an acoustic resonator such as a string or a column of air, which oscillates at numerous modes simultaneously. At the frequencies of each vibrating mode, waves travel in both directions along the string or air column, reinforcing and canceling each other to form standing waves. Interaction with the surrounding air causes audible sound waves, which travel away from the instrument. Because of the typical spacing of the resonances, these frequencies are mostly limited to integer multiples, or harmonics, of the lowest frequency, and such multiples form the harmonic series. The musical pitch of a note is usually perceived as the lowest partial present (the fundamental frequency), which may be the one created by vibration over the full length of the string or air co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Scale On C
Diatonic and chromatic are terms in music theory that are most often used to characterize Scale (music), scales, and are also applied to musical instruments, Interval (music), intervals, Chord (music), chords, Musical note, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the Common practice period, common practice music of the period 1600–1900. These terms may mean different things in different contexts. Very often, ''diatonic'' refers to musical elements derived from the modes and transpositions of the "white note scale" C–D–E–F–G–A–B. In some usages it includes all forms of heptatonic scale that are in common use in Western music (the major, and all forms of the minor). ''Chromatic'' most often refers to structures derived from the twelve-note chromatic scale, which consists of all semitones. Historically, however, it had other senses, referring in Ancient Greek music theory to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
19-tet Scale On C
In music, 19 Tone Equal Temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 63.16 cents (). The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings. 19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12 EDO), so long as the notes are "spelled properly" – that is, with no assumption that the sharp below matches the flat immediately above it (enharmon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspectives Of New Music
''Perspectives of New Music'' (PNM) is a peer-reviewed academic journal specializing in music theory and analysis. It was established in 1962 by Arthur Berger and Benjamin Boretz (who were its initial editors-in-chief). ''Perspectives'' was first published by the Princeton University Press, initially supported by the Fromm Music Foundation.David Carson Berry, "''Journal of Music Theory'' under Allen Forte's Editorship," ''Journal of Music Theory'' 50/1 (2006), 21, n49. The first issue was favorably reviewed in the ''Journal of Music Theory'', which observed that Berger and Boretz had produced "a first issue which sustains such a high quality of interest and cogency among its articles that one suspects the long delay preceding the yet-unborn Spring 1963 issue may reflect a scarcity of material up to their standard". However, as the journal's editorial "perspective" coalesced, Fromm became—in the words of David Gable—disenchanted with the "exclusive viewpoint hatcame to dominate" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |